관계형 DB 정규화 & 함수 종속성

Posted Apr 12, 2025 Updated Apr 15, 2025

By Jaebaek Lee

24 min read

관계형 DB 정규화 & 함수 종속성

DB 설계의 비공식적 원칙

의미 명확하게: 여러 엔터티/관계형 속성을 하나의 릴레이션에 섞지 말 것
중복/Null 값 줄이기: 삽입·삭제·수정 이상(anomalies) 방지
spurious tuples 방지: 비정상적인 JOIN 결과를 피해야함

Semantics of the Relation Attributes

Guideline 1
- 하나의 릴레이션은 하나의 엔터티 타입 또는 하나의 관계 타입에만 대응해야 함
- 여러 개의 엔터티나 관계의 속성을 한 릴레이션에 섞지 말 것

잘못된 예시

학생	학번	수업	담당교수
정재혁	2025001	데이터베이스	정광용
배용남	2025002	운영체제	배용길
조정구	2025003	알고리즘	이택조
조정구	2025003	자료구조	김영남
배용남	2025002	알고리즘	이택조

해당 relation에서 학생, 수업, 담당교수, 학점 등의 속성이 하나의 relation에 섞여 있어, 의미가 명확하지 않음.
두개의 엔터티를 반영하는 relation이기 때문에 업데이트가 일어날 때 마다 오류가 생성될 가능성이 커짐.
중복 정보들이 생김

Redundant info. in Tuples & Update Anomalies

중복 정보의 문제점
- 릴레이션에 중복된 정보가 포함되면, 데이터의 일관성을 유지하기 어려워짐.
- 예: 동일한 수업에 대한 정보가 여러 튜플에 반복적으로 저장될 경우, 수업 정보가 변경될 때 모든 튜플을 업데이트해야 함.

Update Anomalies

삽입 이상 (Insertion Anomaly)
- 새로운 데이터를 삽입할 때 불필요한 정보도 함께 삽입해야 하는 문제.
- 예: 새로운 수업을 추가하려면 담당 교수 정보도 함께 입력해야 함.
삭제 이상 (Deletion Anomaly)
- 데이터를 삭제할 때 의도치 않게 중요한 정보도 함께 삭제되는 문제.
- 예: 특정 학생의 정보를 삭제하면 해당 학생이 수강한 수업 정보도 함께 삭제될 수 있음.
수정 이상 (Modification Anomaly)
- 데이터를 수정할 때 중복된 모든 튜플을 수정해야 하는 문제.
- 예: 특정 수업의 담당 교수가 변경되면, 해당 수업이 포함된 모든 튜플을 수정해야 함.
Guideline 2
- 삽입/삭제/수정 이상이 없도록 설계

Null Values in Tuples

너무 많은 속성을 한 relation에 몰아넣으면 Null 값이 많아질 수 있음
예: 학생 entity에 대해 너무 많은 속성을 부여하면(기숙사 주소, 개인사물함 등) 많은 튜플에 대해 null값이 생김. 해당 속성은 별도 relation으로 분리
Guideline 3
- 자주 NULL이 되는 속성은 분리할 것

Spurious Tuples

잘못된 relation 분해로 인해 JOIN 연산시 원래 없던 데이터 생성
예:
- 잘못된 분해 예시
  Relation 1:
  학생 학번
  정재혁 2025001
  배용남 2025002
  조정구 2025003
  Relation 2:
  수업 담당교수
  데이터베이스 정광용
  운영체제 배용길
  알고리즘 이택조
  자료구조 김영남
  알고리즘 이택조
  위와 같이 relation을 분해한다면 Relation 1과 Relation 2를 JOIN 했을 때, 원래 relation에 없던 튜플이 생성될 수 있음.
  학생 학번 수업 담당교수
  정재혁 2025001 알고리즘 이택조
- 올바른 분해 예시
  Relation 1:
  학생 학번
  정재혁 2025001
  배용남 2025002
  조정구 2025003
  Relation 2:
  학번 수업 담당교수
  2025001 데이터베이스 정광용
  2025002 운영체제 배용길
  2025003 알고리즘 이택조
  2025003 자료구조 김영남
  2025002 알고리즘 이택조
  위와 같이 분해하면, Natural JOIN을 통해 원래 relation을 복구할 수 있음.
Guideline 4
- Relation 분해 시, Natural JOIN을 통해 원래의 relation을 복구할 수 있어야 함.
- 따라서 분해된 Relation은 기본키/왜래키 기준으로만 JOIN

학생	학번
정재혁	2025001
배용남	2025002
조정구	2025003

수업	담당교수
데이터베이스	정광용
운영체제	배용길
알고리즘	이택조
자료구조	김영남
알고리즘	이택조

학생	학번	수업	담당교수
정재혁	2025001	알고리즘	이택조

학생	학번
정재혁	2025001
배용남	2025002
조정구	2025003

학번	수업	담당교수
2025001	데이터베이스	정광용
2025002	운영체제	배용길
2025003	알고리즘	이택조
2025003	자료구조	김영남
2025002	알고리즘	이택조

Functional Dependency

정의
- 릴레이션 R에서 속성 집합 $X$와 $Y$가 있을 때, $X$의 값이 $Y$의 값을 고유하게 결정하면, $Y$는 $X$에 함수적으로 종속되었다(fuctional dependent)고 함.
- 이를 $X → Y$로 표현.
- $t_i[X]=t_j[X] \rightarrow t_i[Y]=t_j[Y], \quad \forall i,j $
- 속성 $X$가 candidate key면 항상 $X → Y$ 성립
- fuctional dependency의 역은 항상 성립하는 것은 아님
- 예: 학번 → 학생 이름 (학번이 고유하면 학번으로 학생 이름을 유일하게 결정 가능)

Inference rules for FDs

$F$
주어진 FD 집합
$F^+$ $F$로부터 도출 가능한 모든 Functional Dependencies(Closure)
예
- 주어진 FD 집합 $F$:
  1. 학번 → {이름, 생일, 전공, 학년}
  2. 전공 → {담당 교수, 과사무실}
- $F^+$ 계산:
  1. 학번 → {이름, 생일, 전공, 학년}
  2. 전공 → {담당 교수, 과사무실}
  3. 학번 → {담당 교수, 과사무실}
notations
- $F \vDash X → Y$: $X → Y$는 F로부터 추론됨
- ${X,Y} → Z \Longleftrightarrow XY → Z$

Inference rules

Reflexivity
- $Y \subseteq X \vDash X → Y$
- 예: {학번, 이름} → 학번
Augmentation
- ${X → Y} \vDash XZ → YZ$
- 예: 학번 → 이름이면, 학번, 수업 → 이름, 수업
Transitivity
- ${X → Y,\ Y → Z} \vDash X → Z$
- 예: 학번 → 이름이고 이름 → 이메일이면, 학번 → 이메일
Decomposition
- ${X → YZ} \vDash X → Y,\ X → Z$
- 예: 학번 → 이름, 이메일이면, 학번 → 이름 및 학번 → 이메일
Union
- ${X → Y,\ X → Z} \vDash X → YZ$
- 예: 학번 → 이름이고 학번 → 이메일이면, 학번 → 이름, 이메일
Pseudotransitivity
- ${X → Y, WY → Z} \vDash WX → Z$
- 예: 학번 → 이름이고 (수업, 이름) → 교수이면, (수업, 학번) → 교수

Closure Computation

속성 집합의 Closure 계산
- 주어진 속성 집합 $X$에 대해, $X^+$는 $X$로부터 FD $F$를 사용해 도출 가능한 모든 속성의 집합.
- $X^+$ 계산 알고리즘:
  1. $X^+ = X$로 초기화
  2. $oldX^+ \leftarrow X^+$로 복사
  3. $F$의 각 FD $Y → Z$에 대해:
    - $Y \subseteq X^+$이면 $Z$를 $X^+$에 추가
  4. 더 이상 추가할 속성이 없을 때($oldX^+ = X^+$)까지 반복
- 예:
  - 주어진 FD 집합 $F$:
    1. 학번 → {이름, 생일, 전공, 학년}
    2. 전공 → {담당 교수, 과사무실}
  - $X = {\text{학번}}$일 때:
    1. 초기화: $X^+ = {\text{학번}}$
    2. 복사: $oldX^+ \leftarrow {\text{학번}}$
    3. 학번 → {이름, 생일, 전공, 학년} 적용:
      $X^+ = {\text{학번, 이름, 생일, 전공, 학년}}$
    4. 전공 → {담당 교수, 과사무실} 적용:
      $X^+ = {\text{학번, 이름, 생일, 전공, 학년, 담당 교수, 과사무실}}$
    5. 반복:
      $oldX^+ = {\text{학번, 이름, 생일, 전공, 학년, 담당 교수, 과사무실}}$
      FD 모두 적용 후에 $oldX^+ = X^+$이기 때문에 알고리즘 종료

Equivalence of sets of FDs

Cover
FD집합 $F$와 $E$에 대해, 다음과 같은 상황에서 $F$는 $E$를 cover한다고 말함:
$\forall FD(e.g. X \rightarrow Y) \in E, \quad X^+ (w.r.t. F) \supseteq Y$
- 예시:
  - $F$:
    1. 학번 → 이름
    2. 이름 → 이메일
  - $E$:
    1. 학번 → 이메일
  - $F$가 $E$를 cover하는지 확인:
    - $X = {\text{학번}}$에 대해 $F$로 $X^+$계산:
      1. 학번 → 이름: $X^+ = {\text{학번, 이름}}$
      2. 이름 → 이메일: $X^+ = {\text{학번, 이름, 이메일}}$
    - $X^+$가 이메일을 포함하므로, $F$ covers $E$.
Equivalance
$F^+$와 $E^+$가 같을 때 두 FD는 같다고 표현함.
Minimal Cover
- FD 집합 $F$의 Minimal Cover는 다음 조건을 만족하는 FD 집합 $G$:
  1. $G$는 $F$와 동등한 Cover를 가짐 ($F^+ = G^+$).
  2. $G$의 모든 FD는 단일 속성의 우변을 가짐.
  3. $G$의 어떤 FD도 제거할 수 없으며, 어떤 FD의 좌변 속성도 제거할 수 없음.
- Minimal Cover 계산 알고리즘:
  1. 모든 FD의 우변을 단일 속성으로 분해.
    $X \in FD \ s.t. \ X\rightarrow \{A_1,\dots,A_n\} \Rightarrow X \rightarrow A_1, \dots X \rightarrow A_n$
  2. FD의 좌변에서 불필요한 속성을 제거.
```
  for each functional dependency X → A in F:
 for each attribute B in X:
     let F_temp = (F - {X → A}) ∪ {(X - {B}) → A}
     if F_temp is equivalent to F:
         replace X → A with (X - {B}) → A in F
```
  3. 불필요한 FD를 제거.
```
  for each remaining functional dependency X → A in F:
 if (F - {X → A}) is equivalent to F:
     remove X → A from F
```
- 예:
  - 주어진 FD 집합 $F$:
    1. 학번 → {이름, 이메일, 학년}
    2. 이름 → 학년
    3. {이름, 학번} → 이메일
  - Minimal Cover 계산:
    1. 모든 FD의 우변을 단일 속성으로 분해:
      - 학번 → 이름
      - 학번 → 이메일
      - 학번 → 학년
      - 이름 → 학년
      - {이름, 학번} → 이메일
    2. FD의 좌변에서 불필요한 속성을 제거:
      - {이름, 학번} → 이메일에서 ‘이름’은 불필요(이미 학번 → 이메일 존재)
      - 이름 제거
      - 결과: 학번 → 이메일(중복)
    3. 불필요한 FD를 제거:
      - 모든 FD를 검토하여 제거 가능한 FD 확인
        학번 → 이름
        학번 → 이메일
        학번 → 학년
        이름 → 학년
      - 학번 → 이름 → 학년의 관계가 있으므로 학번 → 학년은 불필요, 따라서 제거
      - 결과:
        학번 → 이름
        학번 → 이메일
        이름 → 학년

Normalization of Relations

Codd에 의해 주장됨
정규화란 관계형 DB relation을 일련의 테스트를 통해 더 나은 형태로 분해하는 과정
데이터 중복을 최소화하고, 삽입/삭제/갱신 이상(anomalies) 제거하는데 목적을 둠
FD와 기본 키(primary key) 기반으로 수행

※ keys & attributes participating in keys

Superkey
- 릴레이션의 모든 튜플을 고유하게 식별할 수 있는 속성 또는 속성 집합.
Key
- 최소 슈퍼키. 즉, 슈퍼키 중에서 더 이상 속성을 제거할 수 없는 키
- Key가 한개 이상이라면, 각각은 Candidate key
Primary Key
- Candidate key 중에서 선택된 주요 키.
Prime Attribute
- Candidate key에 포함되는 속성

First Normal Form (1NF)

정의
- 릴레이션의 모든 속성이 원자값(atomic value)을 가져야 함.
- 즉, 속성 값이 더 이상 분해되지 않는 단일 값이어야 함.
  - Composite attributes, Multivalued attributes 비허용
조건
1. 릴레이션의 각 속성은 단일 값을 가져야 함.
2. 반복되는 그룹(repeating groups)이 없어야 함.
예시
학생 학번 전공 지도교수
정재혁 2025001 언어학, 인공지능 정광용, 배용길
배용남 2025002 경제학 이선옥
- 위 릴레이션은 수업과 지도교수가 다중값을 가지므로 1NF를 만족하지 않음.
1NF 정규화 방법
1. 문제 속성을 새로운 릴레이션으로 분리
  전공 Relation
  학번 전공
  2025001 언어학
  2025001 인공지능
  2025002 경제학
  지도교수 Relation
  학번 지도교수
  2025001 정광용
  2025001 배용길
  2025002 이선옥
2. 키를 확장해 다중값을 각기 다른 튜플로 표현
  학생 학번 전공 지도교수
  정재혁 2025001 언어학 정광용
  정재혁 2025001 인공지능 배용길
  배용남 2025002 경제학 이선옥
3. 다중값을 여러 column으로 나누기
  학생 학번 전공1 전공2 지도교수1 지도교수2
  정재혁 2025001 언어학 인공지능 정광용 배용길
  배용남 2025002 경제학 Null 이선옥 Null
  해당 경우는 Multivalued의 횟수 최대값이 알려져있을 때만 가능(그렇지 않으면 전공이 3개인 학생이 입력 불가)
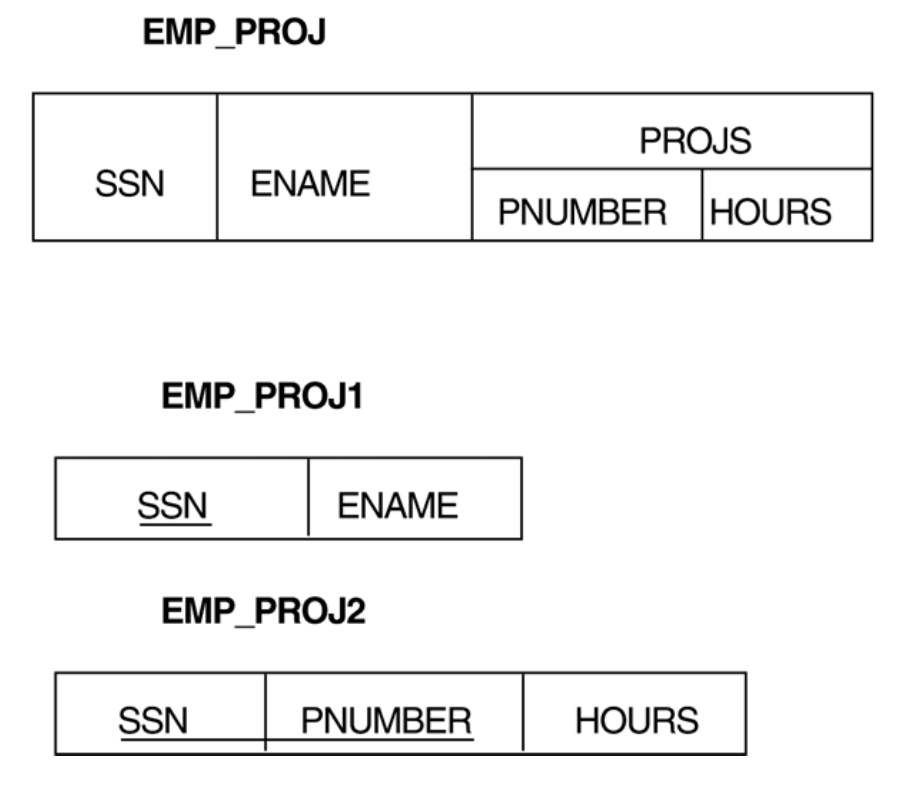
Nested Relation
- 릴레이션의 속성 값이 또 다른 릴레이션(테이블) 형태로 저장된 경우를 말함.
- Nested Relation은 1NF를 위반
- 예시
해당 예시에서 EMP_PROJ라는 relation 내에 PROJS라는 relation 존재.
중첩된 속성을 새 릴레이션으로 분리하고, 기본 키를 전파해서 참조 관계 유지

학생	학번	전공	지도교수
정재혁	2025001	언어학, 인공지능	정광용, 배용길
배용남	2025002	경제학	이선옥

학번	전공
2025001	언어학
2025001	인공지능
2025002	경제학

학번	지도교수
2025001	정광용
2025001	배용길
2025002	이선옥

학생	학번	전공	지도교수
정재혁	2025001	언어학	정광용
정재혁	2025001	인공지능	배용길
배용남	2025002	경제학	이선옥

학생	학번	전공1	전공2	지도교수1	지도교수2
정재혁	2025001	언어학	인공지능	정광용	배용길
배용남	2025002	경제학	Null	이선옥	Null

Second Normal Form (2NF)

정의
- 릴레이션이 1NF를 만족하고, 모든 비프라임 속성이 기본 키에 완전 함수 종속(fully functional dependency)일 때 2NF를 만족한다고 함.
- 즉, 비프라임 속성이 기본 키의 일부가 아닌 전체에 종속되어야 함.
조건
1. 릴레이션이 1NF를 만족해야 함.
2. 비프라임 속성이 기본 키의 부분 집합에 종속되면 안 됨.
예시
학번 수업 교수 학점
2025001 데이터베이스 정광용 3
2025001 현대영시 배용길 3
2025002 알고리즘 이택조 3
- 기본 키: {학번, 수업}
- 비프라임 속성: 교수, 학점
- 문제: 학점은 수업에만 종속되므로 기본 키의 일부(수업)에 종속됨 → 부분 함수 종속 존재
2NF 정규화 방법
1. 부분 함수 종속을 제거하기 위해 릴레이션을 분리
  - 수업 Relation
    수업 학점
    데이터베이스 3
    현대영시 3
    알고리즘 3
  - 학생-수업 Relation
    학번 수업 교수
    2025001 데이터베이스 정광용
    2025001 현대영시 배용길
    2025002 알고리즘 이택조
2. 릴레이션마다 기본 키를 재설정하고, 분리된 릴레이션 간 참조 관계를 유지
- 결과
  - 모든 비프라임 속성이 기본 키에 완전 함수 종속됨.
  - 삽입/삭제/갱신 이상 제거.

학번	수업	교수	학점
2025001	데이터베이스	정광용	3
2025001	현대영시	배용길	3
2025002	알고리즘	이택조	3

수업	학점
데이터베이스	3
현대영시	3
알고리즘	3

학번	수업	교수
2025001	데이터베이스	정광용
2025001	현대영시	배용길
2025002	알고리즘	이택조

Third Normal Form (3NF)

정의
- 릴레이션이 2NF를 만족하고, 비프라임 속성이 기본 키에 이행적 종속(transitive dependency)되지 않을 때 3NF를 만족한다고 함.
- 즉, 비프라임 속성이 다른 비프라임 속성에 종속되면 안 됨.
조건
1. 릴레이션이 2NF를 만족해야 함.
2. 비프라임 속성이 다른 비프라임 속성에 종속되면 안 됨.
예시
학번 지도교수 학과 과사무실
2025001 정광용 컴퓨터공학 2동
2025002 배용길 영어영문학 301동
- 기본 키: 학번
- 비프라임 속성: 학과, 과사무실
- 문제: 과사무실은 학과에 종속되므로 이행적 종속 존재
3NF 정규화 방법
1. 이행적 종속을 제거하기 위해 릴레이션을 분리
  - 학과 Relation
    학과 과사무실
    영어영문학 2동
    컴퓨터공학 301동
  - 학생 Relation
    학번 지도교수 학과
    2025001 정광용 컴퓨터공학
    2025002 배용길 영어영문학
2. 기본 키를 재설정하고, 분리된 릴레이션 간 참조 관계를 유지
- 결과
  - 모든 비프라임 속성이 기본 키에 직접적으로 종속됨.
  - 데이터 중복 제거 및 이상 방지.

학번	지도교수	학과	과사무실
2025001	정광용	컴퓨터공학	2동
2025002	배용길	영어영문학	301동

학과	과사무실
영어영문학	2동
컴퓨터공학	301동

학번	지도교수	학과
2025001	정광용	컴퓨터공학
2025002	배용길	영어영문학

General Definition of 2NF & 3NF

앞서 정의한 2NF/3NF는 “기본 키” 기준이었지만, 후보 키가 여러 개 있을 때는 모든 후보 키에 대해 조건을 만족해야 함
General Definition of 2NF
- 릴레이션 R이 1NF를 만족하고, 모든 비-프라임 속성이 모든 후보 키에 대해 부분 종속되지 않을 때 R은 2NF
General Definition of 3NF
- 릴레이션 R이 1NF를 만족하고, 모든 비-프라임 속성이 모든 후보 키에 대해 이행 종속되지 않을 때 R은 3NF
- 간단한 정리:
  R의 모든 FD $X \rightarrow A$에 대해, $X$가 Superkey거나 $A$가 Prime Attribute이라면 R은 3NF 만족

Boyce-Codd normal form (BCNF)

정의
- 릴레이션 R이 3NF를 만족하고, 모든 FD $X \rightarrow A$에 대해 $X$가 Superkey일 때 R은 BCNF를 만족한다고 함.
- 즉, 모든 결정자(determinant)가 Superkey여야 함.
조건
1. 릴레이션이 3NF를 만족해야 함.
2. 모든 결정자가 Superkey여야 함.
예시
학번 수업 교수
2025001 데이터베이스 정광용
2025001 현대영시 배용길
2025002 알고리즘 이택조
- 기본 키: {학번, 수업}
- 문제: 교수 → 수업이 성립하므로 교수는 결정자지만 Superkey가 아님 → BCNF 위반
BCNF 정규화 방법
1. BCNF 조건을 위반하는 FD를 기준으로 릴레이션을 분리
  - 교수 Relation
    교수 수업
    정광용 데이터베이스
    배용길 현대영시
    이택조 알고리즘
  - 학생-수업 Relation
    학번 수업
    2025001 데이터베이스
    2025001 현대영시
    2025002 알고리즘
2. 기본 키를 재설정하고, 분리된 릴레이션 간 참조 관계를 유지
- 결과
  - 모든 결정자가 Superkey가 됨.
  - 데이터 중복 제거 및 이상 방지.
BCNF와 3NF의 차이
- BCNF는 3NF보다 더 엄격한 조건을 요구함.
- 모든 3NF 릴레이션이 BCNF를 만족하는 것은 아님.
- 예:
  학번 수업 교수
  2025001 데이터베이스 정광용
  2025001 현대영시 배용길
  2025002 알고리즘 이택조
  - 기본 키: {학번, 수업}
  - 교수 → 수업이 성립하므로 BCNF 위반
  - 하지만 교수는 비프라임 속성이므로 3NF는 만족

학번	수업	교수
2025001	데이터베이스	정광용
2025001	현대영시	배용길
2025002	알고리즘	이택조

교수	수업
정광용	데이터베이스
배용길	현대영시
이택조	알고리즘

학번	수업
2025001	데이터베이스
2025001	현대영시
2025002	알고리즘

학번	수업	교수
2025001	데이터베이스	정광용
2025001	현대영시	배용길
2025002	알고리즘	이택조

해당 포스트는 서울대학교 산업공학과 박종헌 교수님의 데이터관리와 분석 25-1학기 강의를 정리한 내용입니다.

데이터베이스

데이터베이스 DB 강의정리

This post is licensed under CC BY 4.0 by the author.