선형대수 개념 정리

Vector

• 벡터란?
  • 벡터 공간 $V$의 원소 (엄밀한 정의)
  • 1-D array of numbers (in Computer Science)
    • 이후 모든 정의는 Computer Science의 방식을 따름
• # of elements in a vector = size(dimension, length) of a vector

\[\vec{x} = [1, 3, 6]^T \in \mathbb{R}^3\]

• 스칼라

\[x_i \in \mathbb{R}\]

Matrices

• 2-D array of numbers
• $A \in \mathbb{R}^{m \times n}$

\[A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}\]

Tensor

• 다차원 배열의 일반화된 개념
• 텐서의 차원 (rank)
  • 스칼라: 0차 텐서
  • 벡터: 1차 텐서
  • 행렬: 2차 텐서
  • 3차원 이상의 텐서
• 텐서의 표기법
  • $\mathcal{T} \in \mathbb{R}^{n_1 \times n_2 \times \cdots \times n_k}$
• 예시:
  • RGB 이미지 텐서
    • 3차원 텐서로 표현
    • 크기: $height \times width \times 3$
    • 각 채널 (R, G, B)은 2차원 행렬
    • 예시: \(\mathcal{I} = \begin{pmatrix} \begin{pmatrix} r_{11} & r_{12} & \cdots & r_{1w} \\ r_{21} & r_{22} & \cdots & r_{2w} \\ \vdots & \vdots & \ddots & \vdots \\ r_{h1} & r_{h2} & \cdots & r_{hw} \end{pmatrix} & \begin{pmatrix} g_{11} & g_{12} & \cdots & g_{1w} \\ g_{21} & g_{22} & \cdots & g_{2w} \\ \vdots & \vdots & \ddots & \vdots \\ g_{h1} & g_{h2} & \cdots & g_{hw} \end{pmatrix} & \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1w} \\ b_{21} & b_{22} & \cdots & b_{2w} \\ \vdots & \vdots & \ddots & \vdots \\ b_{h1} & b_{h2} & \cdots & b_{hw} \end{pmatrix} \end{pmatrix}\)
  • 영상 텐서
    • 비디오 데이터는 4차원 텐서로 표현
      • 크기: $frames \times height \times width \times channels$
      • 각 프레임은 3차원 텐서 (RGB 이미지)
      • 예시: \(\mathcal{V} = \begin{pmatrix} \mathcal{I}_1 \\ \mathcal{I}_2 \\ \vdots \\ \mathcal{I}_f \end{pmatrix}\)

Identity Matrix

• 대각 원소가 모두 1이고 나머지는 0인 행렬
• 항등 행렬 $I \in \mathbb{R}^{n \times n}$

\[I = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}\]

• 항등 행렬의 성질
  • $AI_n = A \ (\forall A \in \mathbb{R}^{m \times n})$
  • $I_mA = A \ (\forall A \in \mathbb{R}^{m \times n})$
  • $I^T = I$
  • $I^{-1} = I$

Diagonal Matrix

• 대각 원소 외의 모든 원소가 0인 행렬
• 대각 행렬 $D \in \mathbb{R}^{n \times n}$

\[D = \begin{pmatrix} d_{11} & 0 & \cdots & 0 \\ 0 & d_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_{nn} \end{pmatrix}\]

• 대각 행렬의 성질
  • $D^T = D$
  • $D^{-1}$는 존재할 경우 대각 행렬
  • $D_1D_2 = D_2D_1$ (대각 행렬 간의 곱셈은 교환 법칙이 성립)
• Also denoted: \(D = \text{diag}(d_{11}, d_{22}, \ldots, d_{nn})\)

Matrix-Matrix multiplication

• 두 행렬 $A \in \mathbb{R}^{m \times n}$, $B \in \mathbb{R}^{n \times p}$의 곱 $C \in \mathbb{R}^{m \times p}$는 다음과 같이 정의됨

\[C = AB = \begin{pmatrix} c_{11} & c_{12} & \cdots & c_{1p} \\ c_{21} & c_{22} & \cdots & c_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ c_{m1} & c_{m2} & \cdots & c_{mp} \end{pmatrix}\]

• 각 원소 $c_{ij}$는 다음과 같이 계산됨

\[c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj}\]

• 행렬 곱셈의 성질
  • 결합 법칙: $A(BC) = (AB)C$
  • 분배 법칙: $A(B + C) = AB + AC$
  • 일반적으로 교환 법칙은 성립하지 않음: $AB \neq BA$
• 예시:
  • $A \in \mathbb{R}^{2 \times 3}$, $B \in \mathbb{R}^{3 \times 2}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}, \quad B = \begin{pmatrix} 7 & 8 \\ 9 & 10 \\ 11 & 12 \end{pmatrix}\] \[AB = \begin{pmatrix} 1 \cdot 7 + 2 \cdot 9 + 3 \cdot 11 & 1 \cdot 8 + 2 \cdot 10 + 3 \cdot 12 \\ 4 \cdot 7 + 5 \cdot 9 + 6 \cdot 11 & 4 \cdot 8 + 5 \cdot 10 + 6 \cdot 12 \end{pmatrix} = \begin{pmatrix} 58 & 64 \\ 139 & 154 \end{pmatrix}\]

Vector-Vector Product

• 내적 (Dot Product)
  • 두 벡터 $\vec{a}, \vec{b} \in \mathbb{R}^n$의 내적은 다음과 같이 정의됨 \(\vec{a} \cdot \vec{b} = \sum_{i=1}^{n} a_i b_i\)
  • 예시: \(\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}\) \(\vec{a} \cdot \vec{b} = 1 \cdot 4 + 2 \cdot 5 + 3 \cdot 6 = 32\)
• 외적 (Cross Product)
  • 두 벡터 $\vec{a}, \vec{b} \in \mathbb{R}^3$의 외적은 다음과 같이 정의됨 \(\vec{a} \times \vec{b} = \begin{pmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix}\)
  • 예시: \(\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad \vec{b} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}\) \(\vec{a} \times \vec{b} = \begin{pmatrix} 2 \cdot 6 - 3 \cdot 5 \\ 3 \cdot 4 - 1 \cdot 6 \\ 1 \cdot 5 - 2 \cdot 4 \end{pmatrix} = \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix}\)

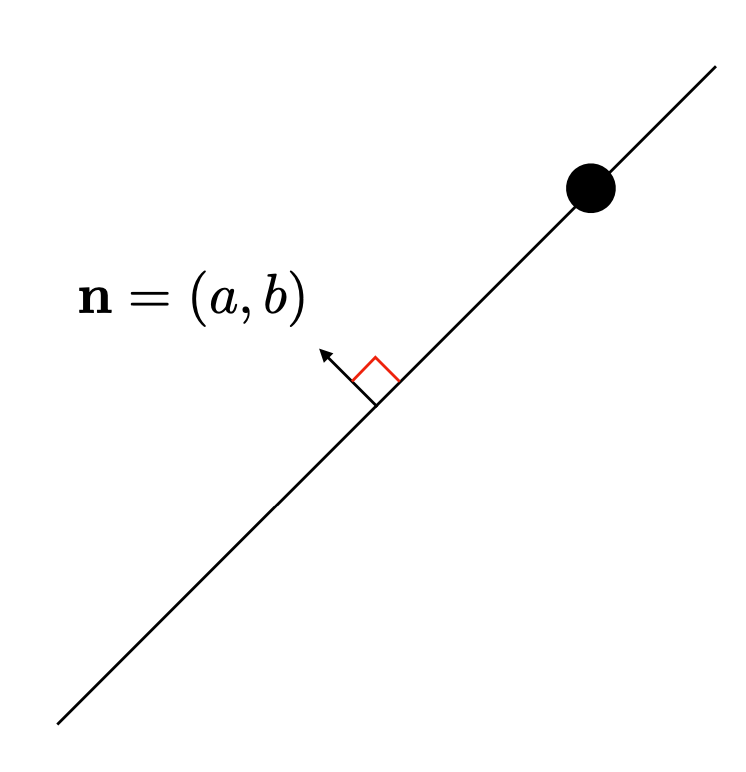
Representing 2D lines via Vector-Vector Product

\[y = ax + b \newline \rightarrow \\{(x, y) | ax+by+c=0\\} \newline \rightarrow (a, b, c) \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = 0\]

Matrix-Vector Product

• $A \in \mathbb{R}^{m\times n}$ 의 행을 중심으로 볼 때:
  • $A$의 각 행을 $\vec{a}_i^T$로 나타낼 수 있음 \(A = \begin{pmatrix} \vec{a}_1^T \\ \vec{a}_2^T \\ \vdots \\ \vec{a}_m^T \end{pmatrix}\)
  • $A\vec{x}$는 각 $\vec{a}_i^T$와 $\vec{x}$의 내적을 포함하는 벡터 \(A\vec{x} = \begin{pmatrix} \vec{a}_1^T \vec{x} \\ \vec{a}_2^T \vec{x} \\ \vdots \\ \vec{a}_m^T \vec{x} \end{pmatrix}\)
• $A \in \mathbb{R}^{m\times n}$ 의 열을 중심으로 볼 때:
  • $A$의 각 열을 $\vec{a}_j$로 나타낼 수 있음 \(A = \begin{pmatrix} \vec{a}_1 & \vec{a}_2 & \cdots & \vec{a}_n \end{pmatrix}\)
  • $A\vec{x}$는 각 $\vec{a}_j$와 $x_j$의 선형결합(linear combination)으로 나타낼 수 있음 \(A\vec{x} = x_1\vec{a}_1 + x_2\vec{a}_2 + \cdots + x_n\vec{a}_n\)

Hadamard Product (Element-wise Product)

• 두 행렬 $A \in \mathbb{R}^{m \times n}$, $B \in \mathbb{R}^{m \times n}$의 Hadamard 곱 $C \in \mathbb{R}^{m \times n}$는 다음과 같이 정의됨

\[C = A \circ B = \begin{pmatrix} a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1n} b_{1n} \\ a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2n} b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{m1} & a_{m2} b_{m2} & \cdots & a_{mn} b_{mn} \end{pmatrix}\]

• 각 원소 $c_{ij}$는 다음과 같이 계산됨

\[c_{ij} = a_{ij} b_{ij}\]

• 예시:
  • $A \in \mathbb{R}^{2 \times 3}$, $B \in \mathbb{R}^{2 \times 3}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}, \quad B = \begin{pmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{pmatrix}\] \[A \circ B = \begin{pmatrix} 1 \cdot 7 & 2 \cdot 8 & 3 \cdot 9 \\ 4 \cdot 10 & 5 \cdot 11 & 6 \cdot 12 \end{pmatrix} = \begin{pmatrix} 7 & 16 & 27 \\ 40 & 55 & 72 \end{pmatrix}\]

Transpose

• 행렬 $A \in \mathbb{R}^{m \times n}$의 전치는 $A^T \in \mathbb{R}^{n \times m}$로 나타내며, $A$의 행과 열을 뒤바꾼 행렬임

\[A^T = \begin{pmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{pmatrix}\]

• 전치 행렬의 성질
  • $(A^T)^T = A$
  • $(A + B)^T = A^T + B^T$
  • $(cA)^T = cA^T \ (\forall c \in \mathbb{R})$
  • $(AB)^T = B^T A^T$
• 예시:
  • $A \in \mathbb{R}^{2 \times 3}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}\] \[A^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}\]

Trace

• 행렬 $A \in \mathbb{R}^{n \times n}$의 대각 원소의 합
• trace $tr(A)$는 다음과 같이 정의됨

\[tr(A) = \sum_{i=1}^{n} a_{ii}\]

• 성질
  • $tr(A + B) = tr(A) + tr(B)$
  • $tr(cA) = c \cdot tr(A) \ (\forall c \in \mathbb{R})$
  • $tr(A^T) = tr(A)$
  • $tr(AB) = tr(BA)$
• 예시:
  • $A \in \mathbb{R}^{3 \times 3}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}\] \[tr(A) = 1 + 5 + 9 = 15\]

Norms

Vector Norms

• 벡터 $\vec{x} \in \mathbb{R}^n$의 norm은 벡터의 크기를 측정하는 방법
• $p$-norm ($L^p$ norm)
  • $p \geq 1$인 경우, $p$-norm은 다음과 같이 정의됨 \(\|\vec{x}\|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}}\)
  • 특수한 경우:
    • $p = 1$: 맨하탄 norm (Manhattan norm) \(\|\vec{x}\|_1 = \sum_{i=1}^{n} |x_i|\)
    • $p = 2$: 유클리드 norm (Euclidean norm) \(\|\vec{x}\|_2 = \left( \sum_{i=1}^{n} x_i^2 \right)^{\frac{1}{2}}\)
    • $p \rightarrow \infty$: 최대 norm (Maximum norm) \(\|\vec{x}\|_\infty = \max_{i} |x_i|\)
      • $p \rightarrow \infty$ 일때 가장 큰 성분이 norm을 결정
    • $p = 0$: 제로 norm (Zero norm) \(\|\vec{x}\|_0 = \lim_{p \to 0} \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}} = \# \\{i \mid x_i \neq 0\\}\)
      • 제로 norm은 엄밀히 말해 norm이 아니며(homogeneity 만족하지 못함), 벡터에서 0이 아닌 원소의 개수를 측정함
        ※ homogeneity: $|\alpha\vec{x}|\ = |\alpha||\vec{x}|$

Matrix Norms

• 행렬 $A \in \mathbb{R}^{m \times n}$의 norm은 행렬의 크기를 측정하는 방법
• 프로베니우스 norm (Frobenius norm)
  • 프로베니우스 norm은 행렬의 각 원소의 제곱합의 제곱근으로 정의됨 \(\|A\|_F = \left( \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2 \right)^{\frac{1}{2}}\)

Linearly Dependent and Independent

• 벡터 집합 $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\}$가 주어졌을 때, 이 벡터들이 선형 독립인지 종속인지를 판단할 수 있음
• 선형 독립 (Linearly Independent)
  • 벡터 집합 $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\}$가 선형 독립이라는 것은, 이 벡터들 사이에 자명하지 않은 선형 결합이 존재하지 않음을 의미
  • 즉, $c_1\vec{v}_1 + c_2\vec{v}_2 + \cdots + c_k\vec{v}_k = \vec{0}$ 일 때, $c_1 = c_2 = \cdots = c_k = 0$ 이어야 함
• 선형 종속 (Linearly Dependent)
  • 벡터 집합 $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\}$가 선형 종속이라는 것은, 이 벡터들 사이에 자명하지 않은 선형 결합이 존재함을 의미
  • 즉, $c_1\vec{v}_1 + c_2\vec{v}_2 + \cdots + c_k\vec{v}_k = \vec{0}$ 일 때, 적어도 하나의 $c_i \neq 0$ 인 경우가 존재함
• 예시:
  • $\vec{v}_1 = \begin{pmatrix} 1 \ 2 \ 3 \end{pmatrix}$, $\vec{v}_2 = \begin{pmatrix} 4 \ 5 \ 6 \end{pmatrix}$, $\vec{v}_3 = \begin{pmatrix} 7 \ 8 \ 9 \end{pmatrix}$인 경우
  • $\vec{v}_1, \vec{v}_2, \vec{v}_3$는 선형 종속임
  • $-3\vec{v}_1 + 3\vec{v}_2 - \vec{v}_3 = \vec{0}$ 이기 때문

Rank of A Matrix

• 행렬 $A \in \mathbb{R}^{m \times n}$의 rank는 행렬의 선형 독립인 행 또는 열 벡터의 최대 개수
• rank $r(A)$는 다음과 같이 정의됨
  • $r(A) = \text{dim}(\text{col space of } A) = \text{dim}(\text{row space of } A)$
• 성질
  • $r(A) \leq \min(m, n)$
  • $r(A) = r(A^T)$
  • $r(AB) \leq \min(r(A), r(B))$
  • $r(A+B) \leq r(A)+r(B)$
• 예시:
  • $A \in \mathbb{R}^{3 \times 3}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}\] \[r(A) = 2\]

Inverse of A Square Matrix

• 역행렬 (Inverse Matrix)
  • 정사각 행렬 $A \in \mathbb{R}^{n \times n}$의 역행렬 $A^{-1}$은 $AA^{-1} = A^{-1}A = I$를 만족하는 행렬
  • 역행렬이 존재하려면 $A$는 가역적 (invertible)이어야 함
  • 역행렬의 성질
    • $(A^{-1})^{-1} = A$
    • $(AB)^{-1} = B^{-1}A^{-1}$
    • $(A^T)^{-1} = (A^{-1})^T$

Span and Projection

Span

• 벡터 집합 $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\}$의 span은 이 벡터들의 선형 결합으로 표현될 수 있는 모든 벡터의 집합
• span $\text{span}(\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\})$는 다음과 같이 정의됨 \(\text{span}(\\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_k\\}) = \\{c_1\vec{v}_1 + c_2\vec{v}_2 + \cdots + c_k\vec{v}_k \mid c_1, c_2, \ldots, c_k \in \mathbb{R}\\}\)
• 예시:
  • $\vec{v}_1 = \begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}$, $\vec{v}_2 = \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix}$인 경우
  • $\text{span}(\{\vec{v}_1, \vec{v}_2\})$는 $\mathbb{R}^2$의 모든 벡터를 포함

Projection

• $\vec{y} \in \mathbb{R}^m$를 $\text{span}(\{x_1, x_2, \ldots, x_n\})$에 Projection한 결과는 다음과 같은 문제로 정의될 수 있음
  \(\arg \min_{\hat{y} \in \text{span}(\\{x_1, x_2, \ldots, x_n\\})} \|\vec{y} - \hat{y}\|_2\)

• $\vec{y}$를 $\text{span}(\{x_1, x_2, \ldots, x_n\})$에 정사영한 결과는 $\hat{y}$로 나타낼 수 있음 \(\hat{y} = X(X^TX)^{-1}X^T\vec{y}\)
• 여기서 $X$는 $\{x_1, x_2, \ldots, x_n\}$를 열 벡터로 가지는 행렬 \(X = \begin{pmatrix} | & | & & | \\ x_1 & x_2 & \cdots & x_n \\ | & | & & | \end{pmatrix}\)
• 예시:
  • $\vec{y} = \begin{pmatrix} 1 \ 2 \ 3 \end{pmatrix}$, $x_1 = \begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}$, $x_2 = \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix}$인 경우
  • $\vec{y}$를 $\text{span}(\{x_1, x_2\})$에 정사영한 결과는 $\hat{y} = \begin{pmatrix} 1 \ 2 \ 0 \end{pmatrix}$

Basis and Dimension

• Basis
  • 벡터 공간 $V$의 기저 (basis)는 $V$의 모든 벡터를 선형 결합으로 표현할 수 있는 선형 독립 벡터들의 집합
  • 기저 $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n\}$는 다음과 같은 성질을 가짐
    • $\text{span}(\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n\}) = V$
    • $\{\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n\}$는 선형 독립
  • 예시:
    • $\mathbb{R}^3$의 표준 기저는 $\{\begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}, \begin{pmatrix} 0 \ 1 \ 0 \end{pmatrix}, \begin{pmatrix} 0 \ 0 \ 1 \end{pmatrix}\}$
• Dimension
  • 벡터 공간 $V$의 차원 (dimension)은 $V$의 기저를 이루는 벡터의 개수
  • $\text{dim}(V)$로 나타내며, $V$의 모든 기저는 동일한 개수의 벡터를 가짐

Orthogonal Matrices

Orthogonal and Orthonormal Vectors

• Orthogonal Vectors
  • 두 벡터 $\vec{u}, \vec{v} \in \mathbb{R}^n$가 직교한다는 것은, 이 두 벡터의 내적이 0임을 의미 \(\vec{u} \cdot \vec{v} = 0\)
• Orthonormal Vectors
  • 두 벡터 $\vec{u}, \vec{v} \in \mathbb{R}^n$가 정규 직교한다는 것은, 이 두 벡터가 직교하고, 각각의 벡터의 norm이 1임을 의미 \(\|\vec{u}\| = 1, \quad \|\vec{v}\| = 1, \quad \vec{u} \cdot \vec{v} = 0\)
  • 예시: \(\vec{u} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \quad \vec{v} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\)

Orthogonal Matrix

• Orthogonal Matrix
  • 행렬 $Q \in \mathbb{R}^{n \times n}$가 직교 행렬이라는 것은, $Q$의 열 벡터들이 서로 직교하고, 각 열 벡터의 norm이 1임을 의미
  • 즉, $Q$의 열 벡터들이 정규 직교 벡터들로 이루어져 있음
  • 직교 행렬의 성질
    • $Q^T Q = QQ^T = I$
    • $Q^{-1} = Q^T$
    • $Q$의 열 벡터와 행 벡터는 모두 정규 직교 벡터들로 이루어져 있음

Rotation Matrix

• 회전 행렬은 벡터를 원점 기준으로 회전시키는 변환을 나타내는 행렬
• 2차원 회전 행렬 $R(\theta) \in \mathbb{R}^{2 \times 2}$는 다음과 같이 정의됨 \(R(\theta) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}\)
• 3차원 회전 행렬은 회전 축에 따라 다르게 정의됨
  • $x$축을 기준으로 회전하는 행렬 $R_x(\theta) \in \mathbb{R}^{3 \times 3}$ \(R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \end{pmatrix}\)
  • $y$축을 기준으로 회전하는 행렬 $R_y(\theta) \in \mathbb{R}^{3 \times 3}$ \(R_y(\theta) = \begin{pmatrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{pmatrix}\)
  • $z$축을 기준으로 회전하는 행렬 $R_z(\theta) \in \mathbb{R}^{3 \times 3}$ \(R_z(\theta) = \begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix}\)
• 회전 행렬의 성질
  • 회전 행렬은 직교 행렬이므로 $R^T R = I$
  • 회전 행렬의 역행렬은 전치 행렬과 같음: $R^{-1} = R^T$
  • 회전 행렬은 행렬식이 1임: $\det(R) = 1$

Special Orthogonal Group

• Special Orthogonal Group $SO(n)$은 $n \times n$ 정사각 행렬들로 이루어진 집합으로, 이 행렬들은 다음 두 조건을 만족함
  1. 행렬의 행과 열이 정규 직교 벡터들로 이루어져 있음
  2. 행렬의 행렬식(determinant)이 1임
• 회전행렬은 $SO(n)$의 원소

Skew Symmetric Matrix

• 전치가 자신의 값에 음을 취한 것과 같은 행렬

\[A^T = -A\]

• 예시:
  • $A \in \mathbb{R}^{3 \times 3}$인 경우

\[A = \begin{pmatrix} 0 & -2 & 3 \\ 2 & 0 & -1 \\ -3 & 1 & 0 \end{pmatrix}\]

• 스큐 대칭 행렬의 성질
  • 대각 원소는 항상 0임
  • $A$와 $B$가 스큐 대칭 행렬이면, $A + B$도 스큐 대칭 행렬임
  • $cA$도 스큐 대칭 행렬임 ($c \in \mathbb{R}$)
  • $A^T A$는 대칭 행렬임

Gram Matrix

• 행렬 $A \in \mathbb{R}^{m \times n}$의 열 벡터들 $\{\vec{a}_1, \vec{a}_2, \ldots, \vec{a}_n\}$이 주어졌을 때, Gram Matrix $G$는 다음과 같이 정의됨

\[G = A^TA = \begin{pmatrix} \vec{a}_1 \cdot \vec{a}_1 & \vec{a}_1 \cdot \vec{a}_2 & \cdots & \vec{a}_1 \cdot \vec{a}_n \\ \vec{a}_2 \cdot \vec{a}_1 & \vec{a}_2 \cdot \vec{a}_2 & \cdots & \vec{a}_2 \cdot \vec{a}_n \\ \vdots & \vdots & \ddots & \vdots \\ \vec{a}_n \cdot \vec{a}_1 & \vec{a}_n \cdot \vec{a}_2 & \cdots & \vec{a}_n \cdot \vec{a}_n \end{pmatrix}\]

• 예시:
  • $A \in \mathbb{R}^{3 \times 2}$인 경우

\[A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix}\] \[\vec{a}_1 = \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix}, \quad \vec{a}_2 = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}\] \[G = \begin{pmatrix} \vec{a}_1 \cdot \vec{a}_1 & \vec{a}_1 \cdot \vec{a}_2 \\ \vec{a}_2 \cdot \vec{a}_1 & \vec{a}_2 \cdot \vec{a}_2 \end{pmatrix} = \begin{pmatrix} 35 & 44 \\ 44 & 56 \end{pmatrix}\]

• Gram Matrix의 성질
  • 대칭 행렬: $G = G^T$
  • 양의 준정부호 행렬: 모든 고유값이 0 이상
  • 벡터 집합이 선형 독립이면, Gram Matrix는 양의 정부호 행렬

Nullspace

• 행렬 $A \in \mathbb{R}^{m \times n}$의 nullspace는 $A\vec{x} = \vec{0}$을 만족하는 모든 $\vec{x} \in \mathbb{R}^n$의 집합
• nullspace $\mathcal{N}(A)$는 다음과 같이 정의됨 \(\mathcal{N}(A) = \\{\vec{x} \in \mathbb{R}^n \mid A\vec{x} = \vec{0}\\}\)
• nullspace의 성질
  • $\mathcal{N}(A)$는 $\mathbb{R}^n$의 부분 공간
  • $A$의 열 벡터들이 선형 독립이면, $\mathcal{N}(A) = \{\vec{0}\}$
  • $A$의 rank와 nullity의 합은 $n$과 같음: $\text{rank}(A) + \text{nullity}(A) = n$
• 예시:
  • $A \in \mathbb{R}^{3 \times 3}$인 경우 \(A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}\) \(\mathcal{N}(A) = \left\\{ \begin{pmatrix} x \\ y \\ z \end{pmatrix} \in \mathbb{R}^3 \mid \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right\\}\) \(\mathcal{N}(A) = \left\\{ \begin{pmatrix} t \\ -2t \\ t \end{pmatrix} \mid t \in \mathbb{R} \right\\}\)

Determinant

• 행렬 $A \in \mathbb{R}^{n \times n}$의 determinant는 $A$가 확장하는 크기를 나타내는 값
• determinant $det(A)$는 다음과 같이 정의됨

\[\text{det}(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^{n} a_{i, \sigma(i)}\]

• 여기서 $S_n$은 $n$개의 원소에 대한 순열 집합, $\text{sgn}(\sigma)$는 순열 $\sigma$의 부호
• 성질
  • $det(A^T) = det(A)$
  • $det(AB) = det(A) \cdot det(B)$
  • $det(A^{-1}) = \frac{1}{det(A)}$ (역행렬이 존재할 경우)
  • $det(cA) = c^n \cdot det(A) \ (\forall c \in \mathbb{R})$
  • $A$가 가역 행렬일 때, $det(A) \neq 0$
• 예시:
  • $A \in \mathbb{R}^{3 \times 3}$인 경우

\[A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}\] \[\text{det}(A) = 1(5 \cdot 9 - 6 \cdot 8) - 2(4 \cdot 9 - 6 \cdot 7) + 3(4 \cdot 8 - 5 \cdot 7) = 0\]

Quadratic Forms

• 벡터 $\vec{x} \in \mathbb{R}^n$와 대칭 행렬 $A \in \mathbb{R}^{n \times n}$에 대해, 이차 형식 $Q(\vec{x})$는 다음과 같이 정의됨 \(Q(\vec{x}) = \vec{x}^T A \vec{x}\)
• 예시:
  • $\vec{x} = \begin{pmatrix} 1 \ 2 \end{pmatrix}$, $A = \begin{pmatrix} 3 & 4 \ 4 & 5 \end{pmatrix}$인 경우 \(Q(\vec{x}) = \begin{pmatrix} 1 & 2 \end{pmatrix} \begin{pmatrix} 3 & 4 \\ 4 & 5 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \end{pmatrix} = 1 \cdot 3 \cdot 1 + 1 \cdot 4 \cdot 2 + 2 \cdot 4 \cdot 1 + 2 \cdot 5 \cdot 2 = 3 + 8 + 8 + 20 = 39\)
• 이차 형식의 성질
  • $Q(\vec{x})$는 항상 실수 값을 가짐
  • $A$가 양의 정부호 행렬이면, $Q(\vec{x}) > 0 \ (\forall \vec{x} \neq \vec{0})$
  • $A$가 양의 준정부호 행렬이면, $Q(\vec{x}) \geq 0 \ (\forall \vec{x})$
  • $A$가 음의 정부호 행렬이면, $Q(\vec{x}) < 0 \ (\forall \vec{x} \neq \vec{0})$
  • $A$가 음의 준정부호 행렬이면, $Q(\vec{x}) \leq 0 \ (\forall \vec{x})$
  • $A$가 부호가 없는 행렬이면, $Q(\vec{x})$는 양수와 음수 모두 가질 수 있음
• 이차 형식의 예시:
  • $\vec{x} = \begin{pmatrix} 1 \ 2 \ 3 \end{pmatrix}$, $A = \begin{pmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{pmatrix}$인 경우 \(Q(\vec{x}) = \begin{pmatrix} 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 1 \cdot 1 \cdot 1 + 2 \cdot 1 \cdot 2 + 3 \cdot 1 \cdot 3 = 1 + 4 + 9 = 14\)

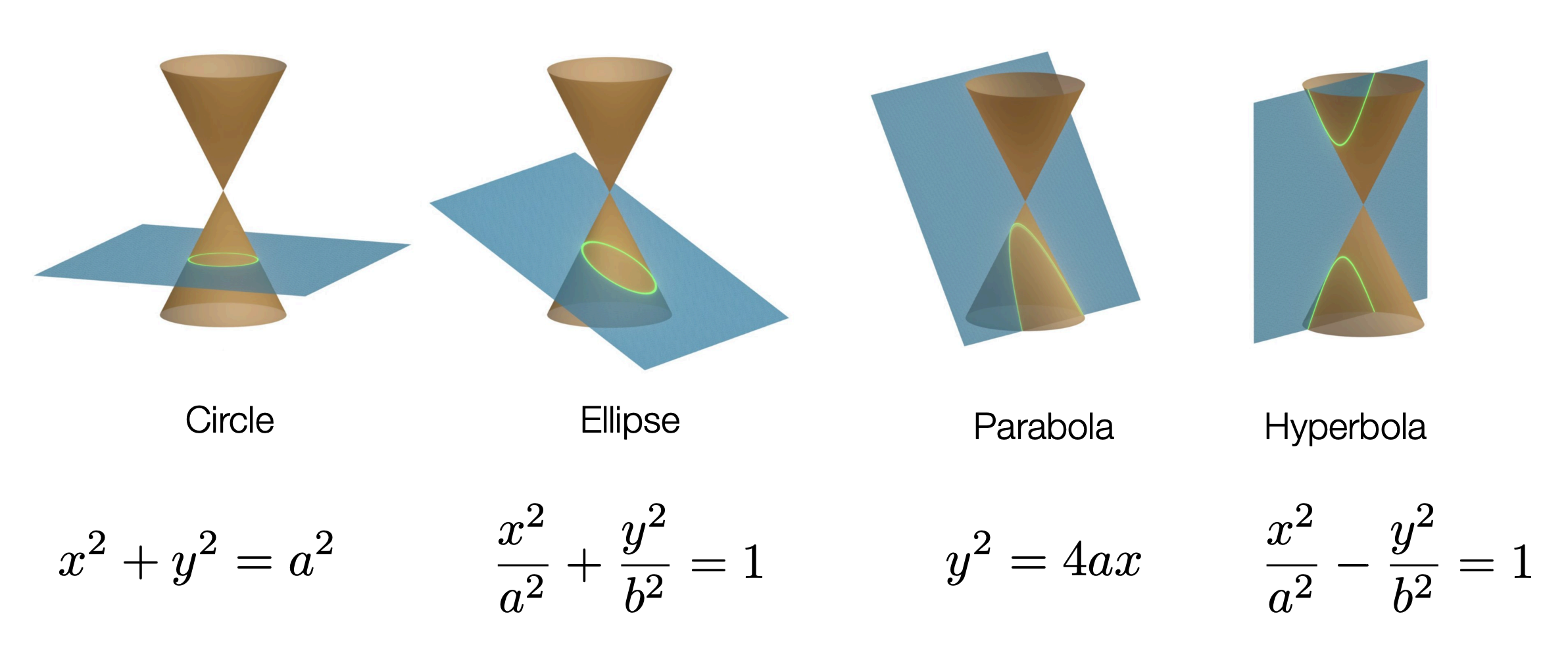위와 같이 다양한 모양의 그래프를 다음과 같은 식으로 일반화해 표현 가능 \(ax^2+bxy+cy^2+dx+ey+f=0\) 이를 이차 형식으로 다시 표현하면 \(\begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} a & \frac{b}{2} & \frac{d}{2} \\ \frac{b}{2} & c & \frac{e}{2} \\ \frac{d}{2} & \frac{e}{2} & f \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = 0\)

Eigenvalues and Eigenvectors

• 행렬 $A \in \mathbb{R}^{n \times n}$의 고유값 $\lambda$와 고유벡터 $\vec{v}$는 다음 조건을 만족함 \(A\vec{v} = \lambda\vec{v}\)
• 여기서 $\vec{v} \neq \vec{0}$, $\lambda \in \mathbb{R}$
• 고유값 $\lambda$는 다음과 같은 특성 방정식의 해로 구할 수 있음 \(\text{det}(A - \lambda I) = 0\)
• 고유벡터 $\vec{v}$는 고유값 $\lambda$에 대응하는 $\text{null}(A - \lambda I)$의 원소
• 예시:
  • $A \in \mathbb{R}^{2 \times 2}$인 경우 \(A = \begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix}\)
  • 고유값 $\lambda$는 다음과 같이 구할 수 있음 \(\text{det}(A - \lambda I) = \text{det}\begin{pmatrix} 4 - \lambda & 1 \\ 2 & 3 - \lambda \end{pmatrix} = (4 - \lambda)(3 - \lambda) - 2 = \lambda^2 - 7\lambda + 10 = 0\)
  • $\lambda = 2, 5$
  • 고유값 $\lambda = 2$에 대응하는 고유벡터 $\vec{v}$는 다음과 같이 구할 수 있음 \((A - 2I)\vec{v} = \begin{pmatrix} 2 & 1 \\ 2 & 1 \end{pmatrix}\vec{v} = \vec{0}\)
  • $\vec{v} = \begin{pmatrix} 1 \ -2 \end{pmatrix}$
  • 고유값 $\lambda = 5$에 대응하는 고유벡터 $\vec{v}$는 다음과 같이 구할 수 있음 \((A - 5I)\vec{v} = \begin{pmatrix} -1 & 1 \\ 2 & -2 \end{pmatrix}\vec{v} = \vec{0}\)
  • $\vec{v} = \begin{pmatrix} 1 \ 1 \end{pmatrix}$
• 고유값과 고유벡터의 성질
  • $A$의 고유값의 합은 $A$의 대각 원소의 합과 같음: $\sum_{i=1}^{n} \lambda_i = \text{tr}(A)$
  • $A$의 고유값의 곱은 $A$의 행렬식과 같음: $\prod_{i=1}^{n} \lambda_i = \text{det}(A)$
  • $A$가 대칭 행렬이면, 모든 고유값은 실수임
  • $A$가 직교 행렬이면, 모든 고유값의 절댓값은 1임

EigenDecomposition

• 행렬 $A \in \mathbb{R}^{n \times n}$는 고유값 분해(EigenDecomposition)할 수 있음
• 고유값 분해는 $A$를 다음과 같이 나타내는 것 \(A = V \Lambda V^{-1}\)
• 여기서 $V$는 $A$의 고유벡터들로 이루어진 행렬, $\Lambda$는 $A$의 고유값들로 이루어진 대각 행렬
• 예시:
  • $A \in \mathbb{R}^{2 \times 2}$인 경우 \(A = \begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix}\)
  • $A$의 고유값은 $\lambda_1 = 2$, $\lambda_2 = 5$
  • $A$의 고유벡터는 $\vec{v}_1 = \begin{pmatrix} 1 \ -2 \end{pmatrix}$, $\vec{v}_2 = \begin{pmatrix} 1 \ 1 \end{pmatrix}$
  • $V$와 $\Lambda$는 다음과 같이 나타낼 수 있음 \(V = \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix}, \quad \Lambda = \begin{pmatrix} 2 & 0 \\ 0 & 5 \end{pmatrix}\)
  • 따라서 $A$는 다음과 같이 고유값 분해할 수 있음 \(A = V \Lambda V^{-1} = \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix} \begin{pmatrix} 2 & 0 \\ 0 & 5 \end{pmatrix} \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix}^{-1}\)
• 고유값 분해의 성질
  • $A$가 대칭 행렬이면, $V$는 직교 행렬이 됨: $V^T V = I$
  • $A$가 대칭 행렬이면, $A$는 다음과 같이 고유값 분해할 수 있음 \(A = Q \Lambda Q^T\)
    • 여기서 $Q$는 $A$의 고유벡터들로 이루어진 직교 행렬, $\Lambda$는 $A$의 고유값들로 이루어진 대각 행렬
  • $A$가 양의 정부호 행렬이면, 모든 고유값은 양수(그 반대도 성립)
• 예시:
  • $A \in \mathbb{R}^{2 \times 2}$인 경우 \(A = \begin{pmatrix} 4 & 1 \\ 1 & 3 \end{pmatrix}\)
  • $A$의 고유값은 $\lambda_1 = 5$, $\lambda_2 = 2$
  • $A$의 고유벡터는 $\vec{v}_1 = \begin{pmatrix} 1 \ 1 \end{pmatrix}$, $\vec{v}_2 = \begin{pmatrix} -1 \ 1 \end{pmatrix}$
  • $Q$와 $\Lambda$는 다음과 같이 나타낼 수 있음 \(Q = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}, \quad \Lambda = \begin{pmatrix} 5 & 0 \\ 0 & 2 \end{pmatrix}\)
  • 따라서 $A$는 다음과 같이 고유값 분해할 수 있음 \(A = Q \Lambda Q^T = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 5 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}\)

Singular Value Decomposition (SVD)

• SVD는 임의의 $m \times n$ 행렬 $A$를 세 개의 행렬의 곱으로 분해하는 방법 \(A = U \Sigma V^T\)
• 여기서 $U \in \mathbb{R}^{m \times m}$, $\Sigma \in \mathbb{R}^{m \times n}$, $V \in \mathbb{R}^{n \times n}$
• $U$와 $V$는 직교 행렬, $\Sigma$는 대각 행렬
• $\Sigma$의 대각 원소는 $A$의 특이값 (singular values)
• $U$의 열 벡터는 $A$의 좌특이 벡터 (left singular vectors)

• $V$의 열 벡터는 $A$의 우특이 벡터 (right singular vectors)

• 특이값 (Singular Values)
  • 특이값은 $\Sigma$의 대각 원소로, $A$의 크기를 나타내는 값
  • 특이값은 항상 0 이상
  • 특이값은 $A^T A$의 고유값의 제곱근으로 구할 수 있음
• 특이 벡터 (Singular Vectors)
  • 좌특이 벡터는 $A A^T$의 고유벡터
  • 우특이 벡터는 $A^T A$의 고유벡터
  • 좌특이 벡터와 우특이 벡터는 각각 $U$와 $V$의 열 벡터
• SVD의 계산 방법
  1. $A^T A$와 $A A^T$의 고유값과 고유벡터를 계산
  2. $A^T A$의 고유벡터를 $V$의 열 벡터로 사용
  3. $A A^T$의 고유벡터를 $U$의 열 벡터로 사용
  4. $A^T A$의 고유값의 제곱근을 $\Sigma$의 대각 원소로 사용
• SVD의 응용
  • 차원 축소 (Dimensionality Reduction)
  • 노이즈 제거 (Noise Reduction)
  • 데이터 압축 (Data Compression)
  • 추천 시스템 (Recommendation Systems)
• 예시
  • $A \in \mathbb{R}^{2 \times 2}$인 경우 \(A = \begin{pmatrix} 4 & 0 \\ 3 & -5 \end{pmatrix}\)
  • $A^T A$와 $A A^T$의 고유값과 고유벡터를 계산 \(A^T A = \begin{pmatrix} 25 & -15 \\ -15 & 25 \end{pmatrix}, \quad A A^T = \begin{pmatrix} 16 & -15 \\ -15 & 34 \end{pmatrix}\)
  • $A^T A$의 고유값은 $\lambda_1 = 40$, $\lambda_2 = 10$
  • $A A^T$의 고유값은 $\lambda_1 = 40$, $\lambda_2 = 10$
  • $A^T A$의 고유벡터는 $\vec{v}_1 = \begin{pmatrix} 1 \ -1 \end{pmatrix}$, $\vec{v}_2 = \begin{pmatrix} 1 \ 1 \end{pmatrix}$
  • $A A^T$의 고유벡터는 $\vec{u}_1 = \begin{pmatrix} 1 \ -1 \end{pmatrix}$, $\vec{u}_2 = \begin{pmatrix} 1 \ 1 \end{pmatrix}$
  • $U$, $\Sigma$, $V$는 다음과 같이 나타낼 수 있음 \(U = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix}, \quad \Sigma = \begin{pmatrix} \sqrt{40} & 0 \\ 0 & \sqrt{10} \end{pmatrix}, \quad V = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}\)
  • 따라서 $A$는 다음과 같이 SVD할 수 있음 \(A = U \Sigma V^T = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \sqrt{40} & 0 \\ 0 & \sqrt{10} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}\)

---

해당 포스트는 서울대학교 컴퓨터공학부 주한별 교수님의 컴퓨터비전 25-1학기 강의를 정리한 내용입니다.