이진 트리

Posted Apr 20, 2025 Updated Apr 23, 2025

By Jaebaek Lee

38 min read

이진 트리

Binary Tree

정의
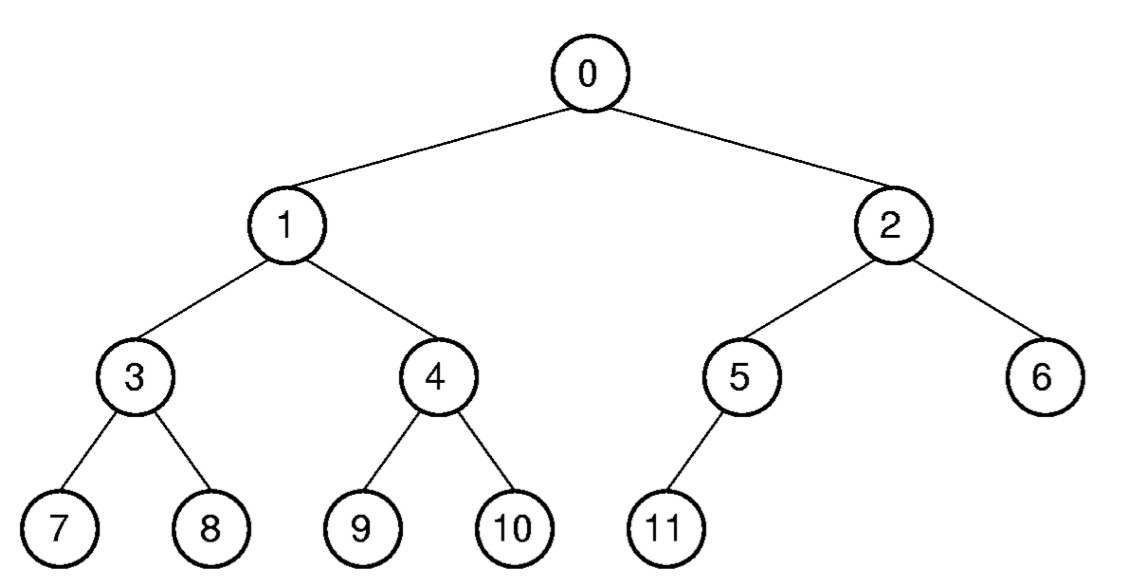
이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식을 가지는 계층적 자료구조.
Notations
- Node: 데이터를 저장하는 기본 단위
- Edge: 노드 간의 연결을 나타내는 선
- Child: 어떤 노드의 자식 노드
- Parent: 어떤 노드의 부모 노드
- Ancestor: 어떤 노드의 조상 노드
- Descendant: 어떤 노드의 자손 노드
- Path: 노드 간의 연결 경로
- Depth: 노드의 깊이
- Height: 트리의 높이
- Level: 노드의 레벨
- Root: 트리의 최상위 노드
- Leaf: 자식 노드가 없는 최하단 노드
- Internal Node: 자식 노드가 있는 노드
- Subtree: 트리의 일부로서 루트 노드와 그 자식 노드들로 구성된 부분 트리

Full Binary Tree

정의
모든 노드가 0개 또는 2개의 자식을 가지는 이진 트리.

Full Binary Tree Theorem

비어있지 않은 Full Binary Tree의 Leaf Node의 개수는 Internal Node의 개수 + 1이다.

증명(수학적 귀납법)
- Base Case: Internal Node가 1개일때, Leaf Node는 2개이다.
- Induction Hypothesis: 어떤 Full Binary Tree의 Internal Node가 $n-1$개일때, Leaf Node는 $n$개이다.
- Inductive Step:
  - $T$가 $n$개의 Internal Node를 갖는 Full Binary Tree라고 가정하자.
  - $T$의 노드 중 자식 노드가 두개인 노드를 선택하여 해당 노드의 자식 노드를 제거하면
    - $T$는 정의에 따라 여전히 Full Binary Tree이고, $n-1$개의 Internal Node를 갖게된다.
    - 따라서 Induction Hypothesis에 의해 Leaf Node는 $n$개가 된다.
  - 이제 $T$에 다시 자식 노드를 2개 추가하면
    - $T$는 다시 Full Binary Tree가 되고, Internal Node는 $n+1$개가 된다.
    - 따라서 Leaf Node는 $n+1$개가 된다.
  - 따라서 Full Binary Tree $T$의 Internal Node의 개수는 $n$일때 Leaf Node의 개수는 $n+1$개이다.
파생 정리
- 비어있지 않은 Binary Tree의 null pointer의 개수는 전체 노드의 개수 - 1이다.
  - 만약 Null pointer를 leaf node로 간주한다면, 해당 트리는 Full Binary Tree가 되고, 모든 노드는 Internal Node가 된다.
  - 따라서 위의 정리에 따라 null pointer의 개수는 전체 노드의 개수 - 1이 된다.

ADT for Binary Tree Node

  
public interface BineNode<E> {
    public E element(); // 노드의 데이터 반환
    public E setElement(E e); // 노드의 데이터 설정

    public BineNode<E> left(); // 왼쪽 자식 노드 반환
    public BineNode<E> right(); // 오른쪽 자식 노드 반환

    public boolean isLeaf(); // 자식 노드가 없는지 확인
}

Traversal

정의
트리의 모든 노드를 방문하는 과정.

Preorder Traversal

정의
루트를 방문하고 왼쪽 서브트리를 방문한 후 오른쪽 서브트리를 방문하는 방법.
순서
1. Root Node 방문
2. Left Subtree 방문
3. Right Subtree 방문

예시

방문 순서: A, B, D, E, C

Postorder Traversal

정의
왼쪽 서브트리를 방문한 후 오른쪽 서브트리를 방문하고 마지막으로 루트를 방문하는 방법.
순서
1. Left Subtree 방문
2. Right Subtree 방문
3. Root Node 방문

예시

방문 순서: D, E, B, C, A

사용 사례
- 계산기 구현
  - 수식을 Postorder Traversal을 사용하여 계산할 수 있다.
  - 예를 들어, 수식 A + B * C는 Postorder Traversal을 사용하여 A, B, C, *, + 순서로 계산할 수 있다

Inorder Traversal

정의
왼쪽 서브트리를 방문한 후 루트를 방문하고 마지막으로 오른쪽 서브트리를 방문하는 방법.
순서
1. Left Subtree 방문
2. Root Node 방문
3. Right Subtree 방문

예시

방문 순서: D, B, E, A, C

Implemeting Traversals

  
public void preorder(BinNode rt) {
    if (rt == null) return;
    visit(rt);
    preorder(rt.left());
    preorder(rt.right());
}

public void postorder(BinNode rt) {
    if (rt == null) return;
    postorder(rt.left());
    postorder(rt.right());
    visit(rt);
}

public void inorder(BinNode rt) {
    if (rt == null) return;
    inorder(rt.left());
    visit(rt);
    inorder(rt.right());
}

Binary Tree Implementation

Recusion
1 2 3 4 int count(BinNode rt) { if (rt == null) return 0; return 1 + count(rt.left()) + count(rt.right()); }
- 이진 트리의 노드 개수를 세는 방법.
- 왼쪽 서브트리와 오른쪽 서브트리의 노드 개수를 재귀적으로 세고, 1(루트 노드)을 더하여 반환.

Two ways of implementing Binary Tree

Single Node Implementation
- Leaf Node와 Internal Node를 구분하지 않고, 모든 노드를 동일하게 처리하는 방법.
- Leaf Node의 자식 노드는 null로 설정.
Two Node Implementation
- Leaf Node와 Internal Node를 구분하여 처리하는 방법.
- Leaf Node를 예외처리하여 자식 노드를 null로 설정하지 않음.

예시(계산기 구현)

  
public interface VarBinNode {
  public boolean isLeaf(); // 자식 노드가 없는지 확인
}

class VarLeafNode implements VarBinNode {
  private Sting operand;
  public VarLeafNode(String val) {
    operand = val;
  }
  public boolean isLeaf() { return true; }
  public String value() { return operand; }
}

class VarIntNode implements VarBinNode {
  private VarBinNode left, right;
  private Character operator;

  public VarIntNode(String op, VarBinNode l, VarBinNode r) {
    operator = op;
    left = l;
    right = r;
  }

  public boolean isLeaf() { return false; }
  public String operator() { return operator; }
  public VarBinNode left() { return left; }
  public VarBinNode right() { return right; }
}

public static void traverse(VarBinNode rt) {
    if (rt == null) return;
    if (rt.isLeaf()) {
        VisitLeafNode(((VarLeafNode) rt).value());
    } else {
        VisitInternalNode(((VarIntNode) rt).operator());
        traverse(((VarIntNode) rt).left());
        traverse(((VarIntNode) rt).right());
    }
}

Comparison

Single Node Implementation
- 장점: 구현이 간단하고, 코드가 짧음.
- 단점: Leaf Node와 Internal Node를 구분하지 않기 때문에, Leaf Node의 자식 노드를 null로 설정해야 함(메모리 오버헤드 발생).
Two Node Implementation
- 장점: Leaf Node와 Internal Node를 구분하여 처리하기 때문에, Leaf Node의 자식 노드를 null로 설정하지 않음(메모리 오버헤드 감소).
- 단점: 구현이 복잡하고, 코드가 길어짐.
Space Overhead = (non data space(pointer space)) / (data space)
- Full Binary Tree Theorem에 의해, Single Node Implementation의 경우
  - Space Overhead = 1 / 2 (null pointer의 개수는 전체 노드의 개수의 절반)
- 만약 Leaf Node가 데이터 저장에만 사용된다면, 오버헤드는 tree가 얼마나 채워졌는지에 따라 달라진다.
예시
- 가정: Full Binary Tree, 모든 노드는 2개의 포인터와 1개의 데이터 저장 공간을 가짐.
  - $p$ = 포인터의 크기, $d$ = 데이터의 크기, $n$ = 노드의 개수일때
  - (총 요구되는 메모리) = $(3p + d) * n$
    각 자식 노드에 2개의 포인터와 1개의 데이터 포인터, 하나의 데이터 저장 공간
  - (포인터 메모리) = $3pn$
  - (오버헤드) = $3pn / (3pn + d) \approx 3/4$ ($p$와 $d$가 유사하면)
- Two Node Implementation
  - (총 요구되는 메모리) = $(\frac{n}{2}) 2p + np + nd$
    - Internal Node만 자식 노드를 위한 포인터를 가짐 : $(\frac{n}{2}) 2p$
    - 모든 노드는 데이터 저장 공간과 포인터를 가짐 : $np + nd$
  - (포인터 메모리) = $np + \frac{n}{2}p$
  - (오버헤드) = $(np + \frac{n}{2}p) / (np + \frac{n}{2}p + nd) \approx 2/3$ ($p$와 $d$가 유사하면)
    - 오버헤드가 줄어듦.

Binary Search Tree

정의
이진 탐색 트리(Binary Search Tree)는 이진 트리의 일종으로, 각 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값이 저장되고, 오른쪽 서브트리에는 해당 노드보다 큰 값이 저장되는 트리.
(따라서 Inorder Traversal을 수행하면 오름차순으로 정렬된 값을 얻을 수 있다.)

ADT for Binary Search Tree

  
class BSTNode<K, E> implements BinNode<E> {
    private K key; // 키 값
    private E element; // 데이터 값
    private BSTNode<K, E> left; // 왼쪽 자식 노드
    private BSTNode<K, E> right; // 오른쪽 자식 노드

    public BSTNode() { left = right = null; }

    public BSTNode(K k, E e) {
        key = k;
        element = e;
        left = null;
        right = null;
    }

    public BSTNode(K k, E e, BSTNode<K, E> l, BSTNode<K, E> r) {
        key = k;
        element = e;
        left = l;
        right = r;
    }

    public K key() { return key; }
    public setKey(K k) { key = k; }

    public E element() { return element; }
    public setElement(E e) { element = e; }

    public BSTNode<K, E> left() { return left; }
    public BSTNode<K, E> setLeft(BSTNode<K, E> l) { left = l; }

    public BSTNode<K, E> right() { return right; }
    public BSTNode<K, E> setRight(BSTNode<K, E> r) { right = r; }
    public boolean isLeaf() { return (left == null && right == null); }
}

ADT for BST implementation for Dictionary

  
public BST<K, E> implemets Dictionary<K, E> {
    private BSTNode<K, E> root; // 루트 노드
    private int size; // 트리의 크기

    public BST() { root = null; size = 0; }

    public void clear() { root = null; size = 0; }

    public void insert(K k, E e) {
        root = inserthelp(root, k, e);
        size++;
    }

    public E remove(K k) {
        E tmp = findhelp(root, k);
        if (tmp != null) {
            root = removehelp(root, k);
            size--;
        }
        return tmp;
    }

    public E find(K k) { return findhelp(root, k); } // 키에 해당하는 데이터 반환

    public E removeAny() {
        if (root != null) {
            E tmp = root.element();
            root = removehelp(root, root.key());
            size--;
            return tmp;
        }
        return null;
    }

    public int size() { return size; }
}

Checking BST

  
boolean checkBST(BSTNode<K, E> rt, Integer low, Integer high) {
    if (rt == null) return true;
    Integer rootKey = rt.key();
    if (rootKey < low || rootKey > high) return false;
    if (!checkBST(rt.left(), low, rootKey-1)) return false;
    return checkBST(rt.right(), rootKey, high);
}

과정
1 2 3 4 5 10 / \ 5 15 / \ / \ 3 7 12 20
- checkBST(10, Integer.MIN_VALUE, Integer.MAX_VALUE)
  - 10은 범위에 포함됨
  - 왼쪽 서브트리 확인: checkBST(5, Integer.MIN_VALUE, 9)
    - 5는 범위에 포함됨
    - 왼쪽 서브트리 확인: checkBST(3, Integer.MIN_VALUE, 4)
      - 3은 범위에 포함됨
      - 왼쪽 서브트리 확인: checkBST(null, Integer.MIN_VALUE, 2) (null)
        true 반환
      - 오른쪽 서브트리 확인: checkBST(null, 3, 4) (null)
        true 반환
      - true 반환
    - 오른쪽 서브트리 확인: checkBST(7, 5, 9)
      - 7은 범위에 포함됨
      - 왼쪽 서브트리 확인: checkBST(null, 5, 6) (null)
        true 반환
      - 오른쪽 서브트리 확인: checkBST(null, 7, 9) (null)
        true 반환
      - true 반환
    - true 반환
  - 오른쪽 서브트리 확인: checkBST(15, 10, Integer.MAX_VALUE)
    - 15는 범위에 포함됨
    - 왼쪽 서브트리 확인: checkBST(12, 10, 14)
      - 12는 범위에 포함됨
      - 왼쪽 서브트리 확인: checkBST(null, 10, 11) (null)
        true 반환
      - 오른쪽 서브트리 확인: checkBST(null, 12, 14) (null)
        true 반환
      - true 반환
    - 오른쪽 서브트리 확인: checkBST(20, 15, Integer.MAX_VALUE)
      - 20은 범위에 포함됨
      - 왼쪽 서브트리 확인: checkBST(null, 15, 19) (null)
        true 반환
      - 오른쪽 서브트리 확인: checkBST(null, 20, Integer.MAX_VALUE) (null)
        true 반환
      - true 반환
    - true 반환
  - true 반환
  - 모든 서브트리가 true이므로, BST임을 확인할 수 있다.

BST search

  
public E findhelp(BSTNode<K, E> rt, K k) {
    if (rt == null) return null;
    if (rt.key().compareTo(k) > 0) {
        return findhelp(rt.left(), k);
    } else if (rt.key().compareTo(k) == 0) {
        return rt.element();
    } else {
        return findhelp(rt.right(), k);
    }
}

과정
1 2 3 4 5 10 / \ 5 15 / \ / \ 3 7 12 20
- findhelp(10, k)
  - k가 10보다 작으면 왼쪽 서브트리 탐색: findhelp(5, k)
  - k가 10보다 크면 오른쪽 서브트리 탐색: findhelp(15, k)
  - k가 10과 같으면 해당 노드 반환: return rt.element()

BST insert

  
public BSTNode<K, E> inserthelp(BSTNode<K, E> rt, K k, E e) {
    if (rt == null) {
        return new BSTNode<K, E>(k, e);
    }
    if (rt.key().compareTo(k) > 0) {
        rt.setLeft(inserthelp(rt.left(), k, e));
    } else {
        rt.setRight(inserthelp(rt.right(), k, e));
    }
    return rt;
}

과정
1 2 3 4 5 10 / \ 5 15 / \ / \ 3 7 12 20
- inserthelp(10, 8, e)
  - 10보다 작으면 왼쪽 서브트리 탐색: inserthelp(5, 8, e)
  - 5보다 크면 오른쪽 서브트리 탐색: inserthelp(7, 8, e)
  - 7보다 크면 오른쪽 서브트리 탐색: inserthelp(null, 8, e)
    - null이면 새로운 노드 생성: return new BSTNode<K, E>(8, e)
  - 왼쪽 서브트리의 오른쪽 자식 노드에 8을 삽입: rt.setRight(new BSTNode<K, E>(8, e))
  - 최종적으로 트리에 8이 삽입됨.
  1 2 3 4 5 6 7 10 / \ 5 15 / \ / \ 3 7 12 20 \ 8
  BST get/remove min/max
```java

public BSTNode<K, E> getMin(BSTNode<K, E> rt) { if (rt.left() == null) return rt; else return getMin(rt.left()); }

public BSTNode<K, E> getMax(BSTNode<K, E> rt) { if (rt.right() == null) return rt; else return getMax(rt.right()); }

```java

public BSTNode<K, E> removeMin(BSTNode<K, E> rt) {
    if (rt.left() == null) return rt.right();
    else rt.setLeft(removeMin(rt.left()));
    return rt;
}

public BSTNode<K, E> removeMax(BSTNode<K, E> rt) {
    if (rt.right() == null) return rt.left();
    else rt.setRight(removeMax(rt.right()));
    return rt;
}

과정
1 2 3 4 5 6 7 10 / \ 5 15 / \ / \ 3 7 12 20 \ 8
- getMin(10)
  - 왼쪽 서브트리 탐색: getMin(5)
    - 왼쪽 서브트리 탐색: getMin(3)
      - 왼쪽 서브트리 탐색: getMin(null) (null)
        null이면 현재 노드 반환: return rt
    - 최종적으로 3 반환.
- getMax(10)
  - 오른쪽 서브트리 탐색: getMax(15)
    - 오른쪽 서브트리 탐색: getMax(20)
      - 오른쪽 서브트리 탐색: getMax(null) (null)
        null이면 현재 노드 반환: return rt
    - 최종적으로 20 반환.
- removeMin(10)
  - 왼쪽 서브트리 탐색: removeMin(5)
    - 왼쪽 서브트리 탐색: removeMin(3)
      - 왼쪽 자식 노드가 null이므로 오른쪽 자식 노드(null) 반환: return rt.right()
    - 5의 왼쪽 서브트리에 null을 설정
  - 최종적으로 3이 제거됨.
- removeMax(10)
  - 오른쪽 서브트리 탐색: removeMax(15)
    - 오른쪽 서브트리 탐색: removeMax(20)
      - 오른쪽 자식 노드가 null이므로 왼쪽 자식 노드(null) 반환: return rt.left()
    - 15의 오른쪽 서브트리에 null을 설정
  - 최종적으로 20이 제거됨.

BST remove

Main Idea
- 삭제할 노드가 Leaf Node인 경우: 해당 노드를 삭제하고 null을 반환.
- 삭제할 노드가 Internal Node인 경우:
  - 오른쪽 서브트리의 최소값을 찾고, 해당 값을 삭제한 후 현재 노드에 대입.

  
public BSTNode<K, E> removehelp(BSTNode<K, E> rt, K k) {
    if (rt == null) return null;
    if (rt.key().compareTo(k) > 0) {
        rt.setLeft(removehelp(rt.left(), k));
    } else if (rt.key().compareTo(k) < 0) {
        rt.setRight(removehelp(rt.right(), k));
    } else {
        if (rt.left() == null) return rt.right();
        else if (rt.right() == null) return rt.left();
        else {
            BSTNode<K, E> tmp = getMin(rt.right());
            rt.setKey(tmp.key());
            rt.setElement(tmp.element());
            rt.setRight(removeMin(rt.right()));
        }
    }
    return rt;
}

과정
1 2 3 4 5 6 7 10 / \ 5 15 / \ / \ 3 7 12 20 \ 8
- removehelp(10, 5)
  - rt.setLeft(removehelp(5, 5))
    - BSTNode<K, E> tmp = getMin(rt.right())
      - 오른쪽 서브트리의 최소값을 찾음: getMin(7)
        7 반환
      - rt.setElement(tmp.element())
        5의 값을 7로 변경
      - rt.setRight(removeMin(rt.right()))
        오른쪽 서브트리에서 7을 제거: removeMin(7)
        7의 위치에 8이 들어감
    - return rt(5)
  - return rt(10)
- 최종적으로 5가 제거됨.
1 2 3 4 5 10 / \ 7 15 / \ / \ 3 8 12 20

Time Complexity of BST Operations

BST Operations
- Search: $O(h)$
- Insert: $O(h)$
- Remove: $O(h)$
- Min/Max: $O(h)$
- Where $h = height\ of\ the\ tree$
- 만약 트리가 균형잡혀 있다면, $h = log\ n$
- 하지만 최악의 경우(편향 트리)에는 $h = O(n)$이 될 수 있다.

Array Implementation of Binary Tree

Complete Binary Tree를 배열로 구현

Position (Index)	0	1	2	3	4	5	6	7	8	9	10	11
Parent	-	0	0	1	1	2	2	3	3	4	4	5
Left Child	1	3	5	7	9	11	-	-	-	-	-	-
Right Child	2	4	6	8	10	-	-	-	-	-	-	-
Left Sibling	-	-	1	-	3	-	5	-	7	-	9	-
Right Sibling	-	2	-	4	-	6	-	8	-	10	-	-

부모, 자식, 형제 노드에 대한 배열을 만들어 이진 트리의 정보를 저장

인덱스 관계 공식

연산	수식
Parent(r)	$\lfloor \frac{r-1}{2} \rfloor$ (단 r>0일 때)
LeftChild(r)	$2r+1$ (단 2r+1< n일 때)
RightChild(r)	$2r+2$ (단 2r+2< n일 때)
LeftSibling(r)	$r-1$ (단 r이 홀수이고 r-1>0일 때)
RightSibling(r)	$r+1$ (단 r이 짝수이고 r+1< n-1일 때)

Priority Queue

정의
우선순위 큐(Priority Queue)는 각 요소가 우선순위를 가지며, 우선순위가 높은 요소가 먼저 처리되는 큐.
일반적인 큐와는 달리, FIFO(First In First Out) 방식이 아닌 우선순위(크기)에 따라 요소가 처리됨.
장점
- 정렬된 배열 - 삽입 $\Theta(n)$, 삭제 $\Theta(1)$
- 정렬되지 않은 배열 - 삽입 $\Theta(1)$, 삭제 $\Theta(n)$
- 우선순위 큐
  - 힙을 사용해 구현시 삽입과 삭제 모두 $\Theta(log\ n)$

Heap

힙(Heap)은 Full Binary Tree의 일종으로, 각 노드가 자식 노드보다 크거나 작은 값을 가지는 특성을 가진 자료구조.

Max Heap: 부모 노드가 자식 노드보다 크거나 같은 값을 가짐.
Min Heap: 부모 노드가 자식 노드보다 작거나 같은 값을 가짐.
이때, BST와는 달리 전체 정렬이 아닌 부분 정렬만 보장됨.
배열을 사용하여 구현.

Max Heap 예시

  
           20
          /  \
         15   10 
        / \   / \
      8   5  7   3

배열 표현: [20, 15, 10, 8, 5, 7, 3]

Max/Min Heap Property
- $n$개 노드 Max/Min Heap에서 Leaf Node의 위치:
  - $\lfloor \frac{n}{2} \rfloor$ 부터 $n-1$까지의 인덱스에 위치
  - 증명
    - 자식 노드의 인덱스는 $2i+1$과 $2i+2$로 표현됨.
    - 따라서 자식 노드가 있기 위해선 $2i+1 \leq n-1$이 성립해야 함.
    - 즉, $i \leq \lfloor \frac{n-2}{2} \rfloor = \lfloor \frac{n}{2} \rfloor - 1$
    - 따라서 자식 노드가 존재할 수 있는 최대 인덱스는 $\lfloor \frac{n}{2} \rfloor - 1$이므로, Leaf Node는 $\lfloor \frac{n}{2} \rfloor$ 부터 $n-1$까지의 인덱스에 위치하게 됨.

Max Heap Implementation

  
public class MaxHeap<E> {
  private E[] Heap; // 힙 배열
  private int size; // 힙의 최대 크기
  private int n; // 힙의 현재 크기

  public MaxHeap(E[] h, int num, int max) 
  { Heap = h; size = max; n = num; }

  public int heapSize() { return n; } // 힙의 크기 반환
  
  public boolean isLeaf(int i) {
    return (i >= n/2 && i < n);
  }
  public int leftChild(int i) {
    assert(i >= 0 && i < n/2) : "Position has no left child";
    return 2*i + 1;
  }
  public int rightChild(int i) {
    assert(i >= 0 && i < n/2) : "Position has no right child";
    return 2*i + 2;
  }
  public int parent(int i) {
    assert(i > 0 && i < n) : "Position has no parent";
    return (i-1)/2;
  }
}

Building Heap

Building Heap Ideas(Max(Min) Heap)
- Max(Min) Heap을 만들기 위해서는 각 노드가 자식 노드보다 크(작)거나 같은 값을 가져야 함.
- Shift Down Method
  - 부모 노드와 자식 노드를 비교하여 부모 노드가 자식 노드보다 작으(크)면 자식 노드와 교환.
  - 마지막 Internal Node부터 시작하여 루트 노드까지 반복.
    - 이때, 루트 노드부터 시작하지 않는 이유는 부모 노드를 먼저 정리해도, 자식 노드가 나중에 바뀌면 힙 성질이 깨질 수 있음
    - 거꾸로 올라가면 그 아래는 정렬되어있으므로, 부모 노드만 정리하면 됨.

  
public void buildHeap() {
    for (int i = n/2 - 1; i >= 0; i--) {
        shiftDown(i);
    }
}

private void shiftDown(int i) {
    assert(i >= 0 && i < n) : "Position is not in heap";
    while (!isLeaf(i)) {
        int j = leftChild(i);
        if (j < n-1 && Heap[j].compareTo(Heap[j+1]) < 0) {
            j++; // j는 오른쪽 자식 노드
        }
        if (Heap[i].compareTo(Heap[j]) >= 0) return; // 부모 노드가 자식 노드보다 크거나 같음
        swap(i, j); // 부모 노드와 자식 노드 교환
        i = j; // 자식 노드로 이동
    }
}

Removing Max/Min

Remove Max 예시

  
           20
          /  \
         15   10 
        / \   / \
      8   5  7   3

최상위 root node(20)를 제거하고, 마지막 노드(3)를 root로 이동.

  
        3
       /  \
      15   10 
     / \   / \
   8   5  7   -

Shift Down을 통해 root node(3)를 적절한 위치로 이동.

  
       15
       /  \
     3    10 
     / \   / \
   8   5  7   -

  
       15
       /  \
     8    10 
     / \   / \
   3   5  7   -

Implementing Remove Max

  
public E removeMax() {
    assert(n > 0) : "Heap is empty";
    E max = Heap[0]; // 최대값 저장
    Heap[0] = Heap[n-1]; // 마지막 노드를 root로 이동
    n--; // 힙 크기 감소
    shiftDown(0); // root 노드에서 Shift Down 수행
    return max; // 최대값 반환
}

public void insert(E x) {
    assert(n < size) : "Heap is full";
    Heap[n] = x; // 새로운 노드 삽입
    n++; // 힙 크기 증가
    while (n > 0 && Heap[parent(n)].compareTo(Heap[n]) < 0) {
        swap(n, parent(n)); // 부모 노드와 교환
        n = parent(n); // 부모 노드로 이동
    }
}

Heap building analysis

시간 복잡도
- Naive approach
  - 모든 노드를 insert하여 힙을 만드는 방법
  - 삽입의 시간 복잡도는 $O(log\ n)$
  - n개의 노드를 삽입하면 $O(n\ log\ n)$
- Shift Down
  - 아래쪽 노드의 shift down은 비교적 적은 시간이 걸림
  - 위쪽 노드의 shift down은 횟수는 많지만, 아래부분이 이미 정렬되어있어 비교적 적은 시간이 걸림
  - level 1을 leaf node라 할 때, level $i$의 노드가 shift down을 수행하면 $i-1$의 시간이 걸림
  - level $i$의 노드 개수는 $\frac{n}{2^{i}}$
  - Heap의 높이는 $h = \lfloor log_{2} n \rfloor$
  - 따라서 전체 수행 시간은 $\sum_{i=1}^{log_{2} n} (i-1) \frac{n}{2^{i}} = \frac{n}{2} \sum_{i=1}^{log_{2} n} (i-1) \frac{1}{2^{i-1}} = \frac{n}{2} 2 - \frac{log_{2} n+2}{2^{log_{2} n}} = O(n)$

Huffman Coding Tree

정의
허프만 코딩 트리는 데이터 압축을 위한 알고리즘으로, 각 문자에 가변 길이의 이진 코드를 할당하여 데이터를 압축하는 방법.
자주 등장하는 문자는 짧은 코드로, 드물게 등장하는 문자는 긴 코드로 표현하여 전체 데이터의 크기를 줄임.
목표
- external path weight를 최소화하는 binary tree 만들기
- external path weight = $\sum_{i=1}^{n} c_i \cdot f_i$
  - $f_i$ = frequency of character(leaf) $i$
  - $c_i$ = depth of character(leaf) $i$(# of bits)
과정
1. 각 문자와 그 빈도를 Leaf Node로 저장
2. Leaf Node를 우선순위 큐에 삽입
3. 우선순위 큐에서 두 개의 노드를 꺼내어 새로운 Internal Node를 생성
4. 생성된 Internal Node를 다시 우선순위 큐에 삽입
5. 모든 노드가 하나의 트리로 합쳐질 때까지 반복
6. 최종적으로 생성된 트리가 허프만 코딩 트리
예시
문자 빈도수
A 5
B 9
C 12
D 13
E 16
F 45
- 우선순위 큐에 삽입
  1 [A(5), B(9), C(12), D(13), E(16), F(45)]
- A와 B를 꺼내어 새로운 Internal Node 생성
  1 [C(12), D(13), (A-B)(14), E(16), F(45)]
- C와 D를 꺼내어 새로운 Internal Node 생성
  1 [(A-B)(14), (C-D)(25), E(16), F(45)]
- (A-B)와 E를 꺼내어 새로운 Internal Node 생성
  1 [(C-D)(25), ((A-B)-E)(30), F(45)]
- (C-D)와 ((A-B)-E)를 꺼내어 새로운 Internal Node 생성
  1 [(((A-B)-E)-(C-D))(55), F(45)]
- (((A-B)-E)-(C-D))와 F를 꺼내어 새로운 Internal Node 생성
  1 [((((A-B)-E)-(C-D))-F)(100)]
- 최종적으로 생성된 트리가 허프만 코딩 트리
  1 2 3 4 5 6 7 8 9 100 1/ \0 55 F(45) 1/ \0 25 30 1/ \0 1/ \0 C D 14 E 1/ \0 A B
  | 문자 | 빈도수 | 허프만 코드 | | —- | —— | ———– | | A | 5 | 1011 | | B | 9 | 1010 | | C | 12 | 111 | | D | 13 | 110 | | E | 16 | 100 | | F | 45 | 0 |
허프만 코드를 encode하기 위해선, 단순히 이어붙이면 됨.
- 예를 들어, “AABBC”는 1011101110101010111111로 인코딩됨.
- 하나의 문자에 대한 허프만 코드는 절대로 다른 문자에 대한 허프만 코드의 prefix가 될 수 없음.
  - 증명
    - 허프만 코드는 이진 트리의 경로로 표현됨.
    - 만약 A의 허프만 코드가 B의 허프만 코드의 prefix라면, A는 B보다 더 깊은 노드에 위치해야 함.
    - 하지만 허프만 코드는 모든 문자가 Leaf Node로 표현되므로, A는 B보다 더 깊은 노드에 위치할 수 없음.
    - 따라서 허프만 코드는 prefix-free property를 만족함.
Expected Cost
- 허프만 코드를 사용하여 인코딩할 때, 허프만 코드의 길이(bits)의 가중평균이 Expected Cost
- $E = \frac{1}{f_T} \sum_{i=1}^{n} c_i \cdot f_i$
  - where $f_T$ = total frequency
- $E$는 허프만 코드를 사용하여 인코딩할 때의 평균 비트 수를 나타냄.
- 위의 예시에서
  - $f_T = 5 + 9 + 12 + 13 + 16 + 45 = 100$
  - $E = \frac{1}{100} (5 \cdot 4 + 9 \cdot 4 + 12 \cdot 3 + 13 \cdot 2 + 16 \cdot 3 + 45 \cdot 1) = \frac{1}{100} (20 + 36 + 36 + 26 + 48 + 45) = \frac{211}{100} = 2.11$
  - 따라서 평균적으로 2.11비트로 인코딩할 수 있음.
  - 이는 기존의 ASCII 코드(8비트)보다 훨씬 적은 비트 수로 인코딩할 수 있음을 의미함.
Uniqueness of Huffman Code
- 주어진 문자 집합과 빈도수에 대해 허프만 코드는 유일하게 결정되지 않음.
- 예를 들어, A와 B를 새로운 Internal Node로 만들 때, A와 B의 순서를 바꿔도 허프만 코드의 성질을 위배하지 않음.
Optimality of Huffman Code
- 허프만 코드는 주어진 문자 집합과 빈도수에 대해 최적의 인코딩을 제공함.
- 증명
  - Contradiction
    - 가정: 최적의 트리 $T$에서, 가장 낮은 빈도수를 가진 두 문자 $x$와 $y$ ($f_x \leq f_y \leq \dots$)가 가장 깊은 노드에 위치하지 않는다고 가정.
      - 즉, $c_z > c_y$인 문자 $z$가 존재.
      - 이 경우, $x$와 $y$가 가장 낮은 빈도수를 가지기 때문에, $f_z \geq f_y$
      - 이때, $y$와 $z$를 교환하면 가중치 변화는 다음과 같음:
        \[\Delta E = f_y c_z + f_z c_y - f_y c_y - f_z c_z = (f_y - f_z)(c_z - c_y)\]
      - $f_y - f_z \leq 0$이고, $c_z - c_y \geq 0$이므로 $\Delta E \leq 0$
      - 즉, external path weight가 감소함.
      - 이는 모순이므로, $x$와 $y$는 가장 깊은 노드에 위치해야 함.
  - Induction
    - Base case: n=2
      - 두 문자가 있을 때, 허프만 트리는 최적
    - Inductive step: n=k+1
      - k개의 문자가 있을 때, 해당하는 허프만 트리가 최적이라고 가정.
      - k+1번째 문자를 추가할 때, k개의 문자 중 가장 낮은 빈도수를 가진 두 문자 $x$와 $y$를 선택.
      - 두 문자를 하나의 새로운 노드 $z$로 치환하고, $x$와 $y$의 빈도수를 더한 값을 $z$의 빈도수로 설정.
      - 이렇게 바꾼 트리는 k개의 문자에 대한 허프만 트리와 같음.
      - 따라서 k+1개의 문자를 포함하는 허프만 트리도 최적임.

문자	빈도수
A	5
B	9
C	12
D	13
E	16
F	45

Search Tree vs Trie(Prefix Tree)

Search Tree
- 이진 탐색 트리(BST)와 같은 자료구조로, 각 노드가 키를 가지고 있음.
Trie
- 문자열을 저장하기 위한 트리 구조로, 각 노드가 문자 하나를 저장함.
- 문자열의 접두사(prefix)를 공유하는 노드들이 같은 경로를 가짐.
- 하나의 경로가 하나의 키가 됨.
  - 한 노드의 모든 후손 노드들은 그 노드의 접두사를 공유함.

해당 포스트는 서울대학교 컴퓨터공학부 강유 교수님의 자료구조 25-1학기 강의를 정리한 내용입니다.

자료구조

This post is licensed under CC BY 4.0 by the author.