Graphs
그래프($G = (V,E)$)는 정점(vertices, $V$)과 정점 사이의 연결인 간선(edges, $E$)으로 구성된 자료구조로, 다양한 문제를 모델링하는 데 사용됨.
- Undirected Graph: 간선이 방향을 가지지 않음
- Directed Graph: 간선이 방향을 가짐
- Weighted Graph: 간선에 가중치가 있음
- Unweighted Graph: 간선에 가중치가 없음
- Path: 정점의 순서대로 연결된 간선들의 집합 $P = (v_1, v_2, \ldots, v_n)$
- 모든 정점이 서로 다른 경우 Simple Path라고 표현함
- Cycle: Path의 시작과 끝 정점이 동일한 경우 $C = (v_1, v_2, \ldots, v_n, v_1)$
- Simple Cycle: Cycle에서 시작 정점과 끝 정점을 제외한 모든 정점이 서로 다른 경우
- Connected Component: 그래프의 모든 정점이 서로 연결되어 있는 부분 그래프
Graph Representation
그래프를 표현하는 방법에는 크게 두 가지가 있음: 인접 행렬(Adjacency Matrix)과 인접 리스트(Adjacency List).
Adjacency Matrix
인접 행렬은 그래프의 정점 간의 연결 관계를 2차원 배열로 표현하는 방법
- Directed Graph
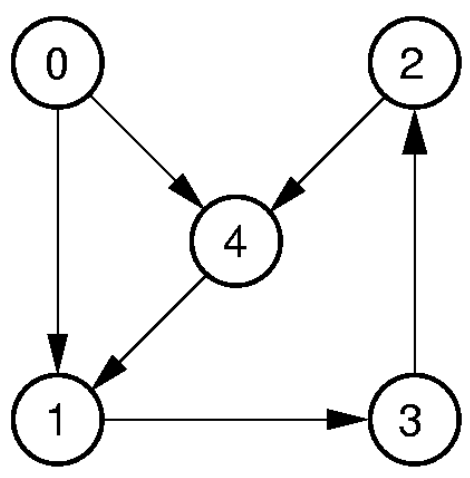
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
- Undirected Graph
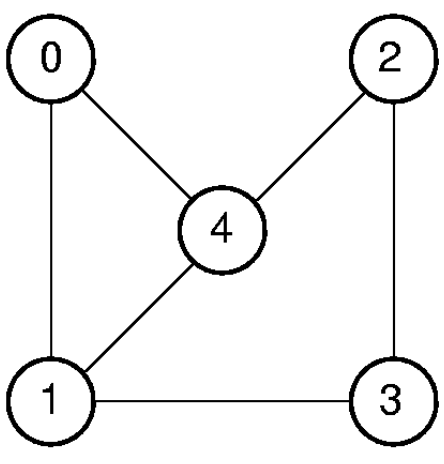
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 | 0 | 0 |
Adjacency List
인접 리스트는 각 정점이 연결된 다른 정점들의 리스트로 표현하는 방법
- Directed Graph
| Index | Value | Neighbors |
|---|---|---|
| 0 | 0 | [1, 4] |
| 1 | 1 | [3] |
| 2 | 2 | [4] |
| 3 | 3 | [2] |
| 4 | 4 | [1] |
- Undirected Graph
| Index | Value | Neighbors |
|---|---|---|
| 0 | 0 | [1, 4] |
| 1 | 1 | [0, 3, 4] |
| 2 | 2 | [3, 4] |
| 3 | 3 | [1, 2] |
| 4 | 4 | [0, 1, 2] |
Representation Cost
Adjacency Matrix: $O( V ^2)$ 모든 정점 간의 연결 관계를 저장하므로, 정점의 개수가 $ V $일 때 $ V ^2$의 공간이 필요함
Adjacency List: $O( V + E )$ 각 정점과 그에 연결된 간선들을 저장하므로, 정점의 개수가 $ V $이고 간선의 개수가 $ E $일 때 $ V + E $의 공간이 필요함 $ E $의 최대값은 $O( V ^2)$ - 증명:
Directed Graph의 경우, 각 정점이 다른 모든 정점과 연결될 수 있으므로 최대 $ V ( V - 1)$개의 간선이 존재할 수 있음 Undirected Graph의 경우, 각 정점 쌍에 대해 간선은 하나만 있으므로 최대 $\frac{ V ( V - 1)}{2}$개의 간선이 존재할 수 있음
- 증명:
따라서 $ E $가 $ V ^2$보다 작은 Sparse Graph에서는 Adjacency List가 더 공간 효율적임 - 반면 간선이 많은 Dense Graph에서는 Adjacency Matrix가 더 공간 효율적임
ADT
1
2
3
4
5
6
7
8
9
10
11
12
13
interface Graph{
public void Init(int n); // 그래프 초기화
public int n(); // 정점의 개수 반환
public int e(); // 간선의 개수 반환
public int first(int v); // 정점 v의 첫 번째 이웃 반환
public int next(int v, int w); // 정점 v의 다음 이웃 w 반환
public void setEdge(int i, int j, int w); // 정점 i와 j 사이에 가중치 w인 간선 추가
public void delEdge(int i, int j); // 정점 i와 j 사이의 간선 제거
public boolean isEdge(int i, int j); // 정점 i와 j 사이에 간선이 있는지 여부 반환
public int weight(int i, int j); // 정점 i와 j 사이의 간선 가중치 반환
public void setMark(int v, int value); // 정점 v에 마크 설정
public int getMark(int v); // 정점 v의 마크 반환
}
Graph Traversal
그래프를 각 정점들을 한번씩만 방문하는 방법을 그래프 탐색(Graph Traversal)이라고 함.
그래프 탐색은 크게 두 가지 방법이 있음: 깊이 우선 탐색(DFS, Depth First Search)과 너비 우선 탐색(BFS, Breadth First Search).
1
2
3
4
5
6
7
8
9
10
11
void graphTraverse(Graph G){
int v;
for(v = 0; v < G.n(); v++){
G.setMark(v, UNVISITED); // 모든 정점의 마크를 UNVISITED로 초기화
}
for(v = 0; v < G.n(); v++){
if(G.getMark(v) == UNVISITED){
doTraverse(G, v); // UNVISITED인 정점에 대해 탐색 시작
}
}
}
Depth First Search (DFS)
깊이 우선 탐색(DFS)은 그래프의 한 정점에서 시작하여 가능한 깊게 탐색한 후, 더 이상 갈 수 없게 되면 마지막으로 방문한 정점으로 돌아가서 다시 탐색을 계속하는 방식
- 시작 정점의 마크를 VISITED로 설정
- 시작 정점의 모든 이웃 정점에 대해
- 이웃 정점의 마크가 UNVISITED인 경우, 해당 정점으로 이동하고 다시 1번부터 반복
- 이웃 정점의 마크가 VISITED인 경우, 해당 정점으로 돌아가서 다음 이웃 정점을 탐색
- 모든 이웃 정점을 탐색한 후, 마지막으로 방문한 정점으로 돌아가서 탐색을 계속함
- 모든 정점이 방문될 때까지 반복함
1
2
3
4
5
6
7
8
void DFS(Graph G, int v){
G.setMark(v, VISITED); // 현재 정점 방문 처리
for(int w = G.first(v); w != -1; w = G.next(v, w)){
if(G.getMark(w) == UNVISITED){ // 이웃 정점이 UNVISITED인 경우
DFS(G, w); // 재귀적으로 DFS 호출
}
}
}
- Cost
시간 복잡도: $O( V + E )$ - 모든 정점과 간선을 한번씩 탐색하므로
공간 복잡도: $O( V )$ - 이웃 정점의 마크가 UNVISITED인 경우, 해당 정점의 마크를 VISITED로 설정하고 큐에 추가
- 이웃 정점의 마크가 VISITED인 경우, 무시하고 다음 이웃 정점을 탐색
- 큐가 비어있을 때까지 2번을 반복함
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void BFS(Graph G, int start){
Queue<Integer> Q = new AQueue<Integer>(G.n()); // 큐 초기화
G.setMark(start, VISITED); // 시작 정점 방문 처리
Q.enqueue(start); // 시작 정점을 큐에 추가
while(!Q.isEmpty()){
int v = Q.dequeue(); // 큐에서 정점 꺼내기
for(int w = G.first(v); w < G.n(); w = G.next(v, w)){
if(G.getMark(w) == UNVISITED){ // 이웃 정점이 UNVISITED인 경우
G.setMark(w, VISITED); // 이웃 정점 방문 처리
Q.enqueue(w); // 이웃 정점을 큐에 추가
}
}
}
}
- Cost
시간 복잡도: $O( V + E )$ - 모든 정점과 간선을 한번씩 탐색하므로
공간 복잡도: $O( V )$ 큐에 최대 $ V $개의 정점이 쌓일 수 있음
Topological Sort
위상 정렬(Topological Sort)은 Directed Acyclic Graph(DAG)에서 정점들을 순서대로 나열하는 방법으로, 각 정점의 선행 조건을 만족하는 순서로 정렬함.
주어진 작업들이 있을때, 선행 작업이 완료된 후에만 수행할 수 있는 작업들의 순서를 결정하는 데 사용됨.(예: J2는 J1 이후에 시작해야 하고 J4는 J2, J3 이후에 시작해야 한다면 J1, J2, J3, J4 순서로 작업을 수행해야 함)
DFS 기반 Topological Sort
DFS를 수행하며, 각 정점을 방문할 때마다 해당 정점을 순서 리스트에 추가함.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void topSort(Graph G){
for(int i = 0; i < G.n(); i++){
G.setMark(i, UNVISITED); // 모든 정점의 마크를 UNVISITED로 초기화
}
for (int i = 0; i < G.n(); i++){
if(G.getMark(i) == UNVISITED){
tophelp(G, i); // UNVISITED인 정점에 대해 DFS 수행
}
}
}
void tophelp(Graph G, int v){
G.setMark(v, VISITED); // 현재 정점 방문 처리
for(int w = G.first(v); w < G.n(); w = G.next(v, w)){
if(G.getMark(w) == UNVISITED){ // 이웃 정점이 UNVISITED인 경우
tophelp(G, w); // 재귀적으로 DFS 호출
}
}
order.add(v); // 현재 정점을 순서 리스트에 추가
}
- 최종적으로는
order리스트에 정점들이 역순으로 저장됨. 따라서order.reverse()를 호출하여 올바른 순서로 정렬함.
Queue 기반 Topological Sort(Kahn’s Algorithm)
Kahn’s Algorithm은 위상 정렬을 수행하기 위해 큐를 사용하는 방법
- 각 정점이 얼마나 많은 간선이 들어오는지 (indegree) 세고
- indegree가 0인 정점은 바로 출력(= 그 정점은 선행 조건이 없음)
- 그 정점과 연결된 간선을 제거 (즉, 그 정점이 다른 정점의 선행 조건이었다면 그 조건을 제거)
- 새로운 indegree 0 정점이 생기면 queue에 넣음
- 이 과정을 반복해 전체 정점을 출력
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void topsort(Graph G) {
Queue<Integer> Q = new AQueue<Integer>(G.n());
int[] Count = new int[G.n()];
// 진입 차수 계산
for (int v = 0; v < G.n(); v++)
for (int w = G.first(v); w < G.n(); w = G.next(v, w))
Count[w]++;
// 진입 차수 0인 정점 queue에 삽입
for (int v = 0; v < G.n(); v++)
if (Count[v] == 0) Q.enqueue(v);
// 위상 정렬
while (Q.length() > 0) {
int v = Q.dequeue();
order.add(v); // 현재 정점을 순서 리스트에 추가
for (int w = G.first(v); w < G.n(); w = G.next(v, w)) {
Count[w]--; // 해당 정점의 진입 차수 감소
if (Count[w] == 0)
Q.enqueue(w); // 진입 차수가 0이 된 정점을 queue에 추가
}
}
}
Shortest Path
최단 경로 문제는 그래프에서 두 정점 사이의 최단 경로를 찾는 문제.
- 두 정점 간 최단 경로 찾기
- 한 정점에서 다른 모든 정점까지의 최단 경로 찾기
- 모든 정점 간 최단 경로 찾기
- $\delta(u, v)$: 정점 $u$에서 정점 $v$까지의 최단 경로의 길이
- $w(u, v)$: 정점 $u$에서 정점 $v$까지의 간선 가중치
Dijkstra’s Algorithm
Dijkstra’s Algorithm은 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘.
- 입력: 가중치가 있는 Directed Graph $G = (V, E)$와 시작 정점 $s \in V$
- 시작 정점 $s$의 거리를 0으로 설정하고, 나머지 정점의 거리를 무한대로 설정
- 모든 정점을 방문하지 않은 상태로 초기화
- 방문하지 않은 정점 중에서 거리가 가장 짧은 정점을 선택
- 선택한 정점에서 인접한 모든 정점에 대해
- 선택한 정점에서 인접한 정점까지의 거리를 계산
- 계산된 거리 = 선택한 정점의 거리 + 선택한 정점과 인접 정점 사이의 간선 가중치
- 계산된 거리가 해당 인접 정점의 현재 거리보다 작으면, 해당 인접 정점의 거리를 업데이트
- 선택한 정점을 방문 처리
- 모든 정점을 방문할 때까지 3번부터 반복함
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void dijkstra(Graph G, int s, int[] D){
for (int v = 0; v < G.n(); v++){
D[v] = Integer.MAX_VALUE; // 모든 정점의 거리를 무한대로 초기화
}
D[s] = 0; // 시작 정점의 거리를 0으로 설정
for (int i = 0; i < G.n(); i++){
int v = minVertex(G, D); // 거리가 가장 짧은 정점 선택
G.setMark(v, VISITED); // 선택한 정점 방문 처리
if (D[v] == Integer.MAX_VALUE) break; // 더 이상 방문할 정점이 없으면 종료
for (int w = G.first(v); w < G.n(); w = G.next(v, w)){
if (D[w] > D[v] + G.weight(v, w)){ // 선택한 정점에서 인접한 정점까지의 거리가 더 짧은 경우
D[w] = D[v] + G.weight(v, w); // 인접 정점의 거리 업데이트
}
}
}
}
- Cost:
minVertex로 가장 짧은 거리의 정점을 선택하고, 선택된 정점의 모든 이웃 정점을 탐색하는 과정 두가지로 구성- 모든 테이블을 순회하여 최소값을 찾는 경우:
모든 정점의 D값을 순회하여 최소값을 찾는 경우, 시간 복잡도는 $O(V )$ minVertex함수는 모든 정점에 대해 수행되므로 $O(V ^2)$ 각 정점의 이웃 정점을 relax하는 과정(거리를 확인하고 갱신하는 과정)은 모든 간선을 한번씩 탐색하므로, 시간 복잡도는 $O( E )$ 따라 전체 시간 복잡도는 $O( V ^2 + E )$ 보통 $ E $가 $ V ^2$보다 작으므로, 최종적으로 $O( V ^2)$로 표현됨
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int minVertex(Graph G, int[] D){
int v = 0; // 미방문 정점 초기화
for (int i = 1; i < G.n(); i++){
if (G.getMark(i) == UNVISITED){
v = i; // 첫 번째 미방문 정점으로 설정
break;
}
}
for (int i = 0; i < G.n(); i++){
if (G.getMark(i) == UNVISITED && D[i] < D[v]){
v = i; // 현재 정점이 미방문 상태이고, 거리가 더 짧은 경우
}
}
return v; // 가장 짧은 거리를 가진 미방문 정점 반환
}
- min-heap(우선순위 큐)를 사용하는 경우:
우선순위 큐를 사용하여 최소값을 찾는 경우, 시간 복잡도는 $O(\log V )$ 모든 정점에 대해 minVertex를 호출하므로 $O(V \log V )$ D값이 줄어들면 heap에서 다시 정렬하는 과정이 필요하므로, 각 정점의 이웃 정점을 relax하는 과정은 $O(E \log V )$ 따라서 전체 시간 복잡도는 $O(( V + E ) \log V )$
1
2
3
4
5
6
7
8
9
int minVertex(Graph G, PriorityQueue<Integer> pq){
while (!pq.isEmpty()){
int v = pq.poll(); // 우선순위 큐에서 최소값을 가진 정점 꺼내기
if (G.getMark(v) == UNVISITED){
return v; // 미방문 정점 반환
}
}
return -1; // 모든 정점이 방문된 경우
}
Correctness of Dijkstra’s Algorithm
- Claim: Dijkstra’s Algorithm에서 정점 $u$가 집합 $S$에 포함될 때, $d(u,s) = \delta(s, u)$, 즉 $u$까지의 최단 거리가 확정
- $d(u,s)$: Dijkstra’s Algorithm에서 정점 $u$까지의 거리
- $\delta(s, u)$: 그래프에서 정점 $s$에서 정점 $u$까지의 최단 경로의 길이
- Proof by Induction
- Base Case: 시작 정점 $s$는 집합 $S$에 포함되며, $d(s,s) = \delta(s, s) = 0$이므로 성립
- Inductive Step: 정점 $u$가 집합 $S$에 포함될 때, $d(s,u) = \delta(s, u)$이 성립한다고 가정
- $S$ 바깥에서, $d(s,v)$값이 가장 작은 정점 $v$를 선택
- $S$와 $S$ 바깥의 집합 $S’$ 경계의 첫 정점 쌍 $(x, y)$를 선택
- 이 경우 relaxation을 통해 $d(s,y) \leq d(s,x) + w(x, y)$가 성립함
- Induction Hypothesis에 의해 $d(s,x) = \delta(s, x)$이므로, $d(s,y) \leq \delta(s, x) + w(x, y)$
- $x \to y$는 $S$의 내부와 $y$를 연결하는 첫 번째 간선이므로, $d(s,y) \leq \delta(s, x) + w(x, y) = \delta(s, y)$이 성립함
- 이때 첫번째 가정에 따라 $d(s,v) \leq d(s,y) = \delta(s, y)$
- $x \to y$가 $S$의 내부와 $y$를 연결하는 첫 번째 간선이므로, $\delta(s, y) \leq \delta(s, v)$이 성립함
- 따라서 $d(s,v) \leq d(s,y) = \delta(s, y) \leq \delta(s, v)$이 성립함
- 정의상 $\delta(s, v) \leq d(s,v)$이므로, $d(s,v) = \delta(s, v)$이 성립함
Minimum Spanning Tree (MST)
최소 신장 트리(Minimum Spanning Tree, MST)는 가중치가 있는 그래프에서 모든 정점을 포함하면서 Cycle이 없고 가중치의 합이 최소인 트리를 찾는 문제.
- 해가 유일하지 않음
- 하지만 해가 존재하는 경우, 모든 해의 가중치 합은 동일함
- 가중치의 합이 최소라는 것은, 사이클이 없음을 보장함
- 만약 사이틀이 있으면, 사이클의 간선 중 하나를 제거하여 가중치의 합을 줄일 수 있음
- 따라 MST는 Cycle이 없는 트리임
Prim’s Algorithm
시작 정점에서부터 인접한 정점 중 가중치가 가장 작은 간선을 선택하여 트리를 확장하는 방식(Greedy Approach)
- 시작 정점의 마크를 VISITED로 설정하고, 해당 정점을 MST에 추가
- MST에 포함되지 않은 정점 중에서, MST에 포함된 정점과 연결된 간선 중 가중치가 가장 작은 간선을 선택
- 선택한 간선의 다른 정점을 MST에 추가하고, 해당 정점의 마크를 VISITED로 설정
- 모든 정점이 MST에 포함될 때까지 2번부터 반복함
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void Prim(Graph G, int s, int[] D, int[] V){ // G: 그래프, s: 시작 정점, D: 거리 배열, V: 부모 정점 배열
int v, w;
for (v = 0; v < G.n(); v++){
D[v] = Integer.MAX_VALUE; // 모든 정점의 거리를 무한대로 초기화
}
D[s] = 0; // 시작 정점의 거리를 0으로 설정
for (int i = 0; i < G.n(); i++){
v = minVertex(G, D); // 거리가 가장 짧은 정점 선택
G.setMark(v, VISITED); // 선택한 정점 방문 처리
if (v != s) {
AddEdgeToMST(V[v], v); // MST에 간선 추가
}
if (D[v] == Integer.MAX_VALUE) break; // 더 이상 방문할 정점이 없으면 종료
for (w = G.first(v); w < G.n(); w = G.next(v, w)){
if (D[w] > G.weight(v, w)){ // 선택한 정점에서 인접한 정점까지의 거리가 더 짧은 경우
D[w] = G.weight(v, w); // 인접 정점의 거리 업데이트
V[w] = v; // 인접 정점의 부모 정점을 선택한 정점으로 설정
}
}
}
}
- Cost: Dijkstra’s Algorithm와 유사하게, Prim’s Algorithm도 모든 정점에 대해
minVertex를 호출하고, 선택된 정점의 모든 이웃 정점을 relax하는 과정으로 구성됨. 따라서 시간 복잡도는 $O( V ^2 + E )$ 또는 $O(( V + E ) \log V )$로 표현됨.
Correctness of Prim’s Algorithm
- Claim: Prim’s Algorithm에서 매 단계에서 선택하는 간선을 포함하는 트리는 반드시 어떤 MST와 동일한 비용을 갖는 트리의 부분 집합임
- Proof by Induction
- Base Case:
- Prim’s Algorithm이 선택한 첫번째 간선 $e = (u, v)$와 어떤 MST $T^*$에 대해
- $e \in T^$, 즉 $T^$에 간선 $e$가 포함됨
이미 $e$를 포함하므로 만족 - $e \notin T^$, 즉 $T^$에 간선 $e$가 포함되지 않음
이 경우, $T^*$에 $e$를 추가하면 Cycle이 생김- Cycle 내에는 $u$를 포함하는 간선 $f$가 존재함
- Prim’s Algorithm은 최소 비용 간선을 선택했으므로, $w(e) \leq w(f)$
- $T’ = T^* - f + e$는 $T^$와 동일한 정점 집합을 가지며, $w(T’) = w(T^) - w(f) + w(e) \leq w(T^*)$
- 이때 $T^$는 MST이므로, $w(T’) = w(T^)$가 성립함
- 따라서 $T’$는 MST이고 $T’$에 $e$가 포함됨
- $e \in T^$, 즉 $T^$에 간선 $e$가 포함됨
- Prim’s Algorithm이 선택한 첫번째 간선 $e = (u, v)$와 어떤 MST $T^*$에 대해
- Inductive Step: $k-1$번째 단계까지 Prim’s Algorithm이 선택한 간선들을 어떤 MST $T^*$의 부분 집합으로 가정
- Prim’s Algorithm이 $k$번째 단계에서 선택한 간선 $g = (x, y)$에 대해
- $g \in T^$, 즉 $T^$에 간선 $g$가 포함됨
- 이미 $g$를 포함하므로 만족
- $g \notin T^$, 즉 $T^$에 간선 $g$가 포함되지 않음
- 이 경우, $T^*$에 $g$를 추가하면 Cycle이 생김
- Cycle 내에는 $S$와 $V\not{S}$를 잇는 간선 $h$가 존재함
- Prim’s Algorithm은 최소 비용 간선을 선택했으므로, $w(g) \leq w(h)$
- $T’ = T^* - h + g$는 $T^$와 동일한 정점 집합을 가지며, $w(T’) = w(T^) - w(h) + w(g) \leq w(T^*)$
- 이때 $T^$는 MST이므로, $w(T’) = w(T^)$가 성립함
- 따라서 $T’$는 MST이고 $T’$에 $g$가 포함됨
- $g \in T^$, 즉 $T^$에 간선 $g$가 포함됨
- Prim’s Algorithm이 $k$번째 단계에서 선택한 간선 $g = (x, y)$에 대해
- Base Case:
Kruskal’s Algorithm
Kruskal’s Algorithm은 그래프의 간선을 가중치 순으로 정렬한 후, Cycle이 생기지 않도록 간선을 선택하여 MST를 구성하는 방식
- 그래프의 모든 간선을 가중치 순으로 정렬
- 최소 가중치의 간선부터 선택
- 해당 간선의 두 정점이 같은 트리에 속하지 않으면, 해당 간선을 MST에 추가
- MST가 완성될 때까지 2번부터 반복함
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void Kruskal(Graph G, int[] D, int[] V){
List<Edge> edges = new ArrayList<>();
for (int v = 0; v < G.n(); v++){
for (int w = G.first(v); w < G.n(); w = G.next(v, w)){
if (v < w) { // 간선 중복 방지
edges.add(new Edge(v, w, G.weight(v, w)));
}
}
}
Collections.sort(edges); // 간선을 가중치 순으로 정렬
for (Edge edge : edges){
int u = edge.u;
int v = edge.v;
if (Find(u) != Find(v)){ // Cycle이 생기지 않는 경우
Union(u, v); // 두 정점을 같은 트리로 합침
AddEdgeToMST(u, v); // MST에 간선 추가
}
}
}
Cost: 간선을 정렬하는 과정이 $O( E \log E )$이고, 각 간선에 대해 Union-Find를 수행하는 과정이 $O( E \alpha( V ))$이므로, 전체 시간 복잡도는 $O( E \log E + E \alpha( V ))$로 표현됨. 대부분의 경우 $ E \log E $(간선 정렬)이 지배적이므로, $O( E \log E )$
해당 포스트는 서울대학교 컴퓨터공학부 강유 교수님의 자료구조 25-1학기 강의를 정리한 내용입니다.