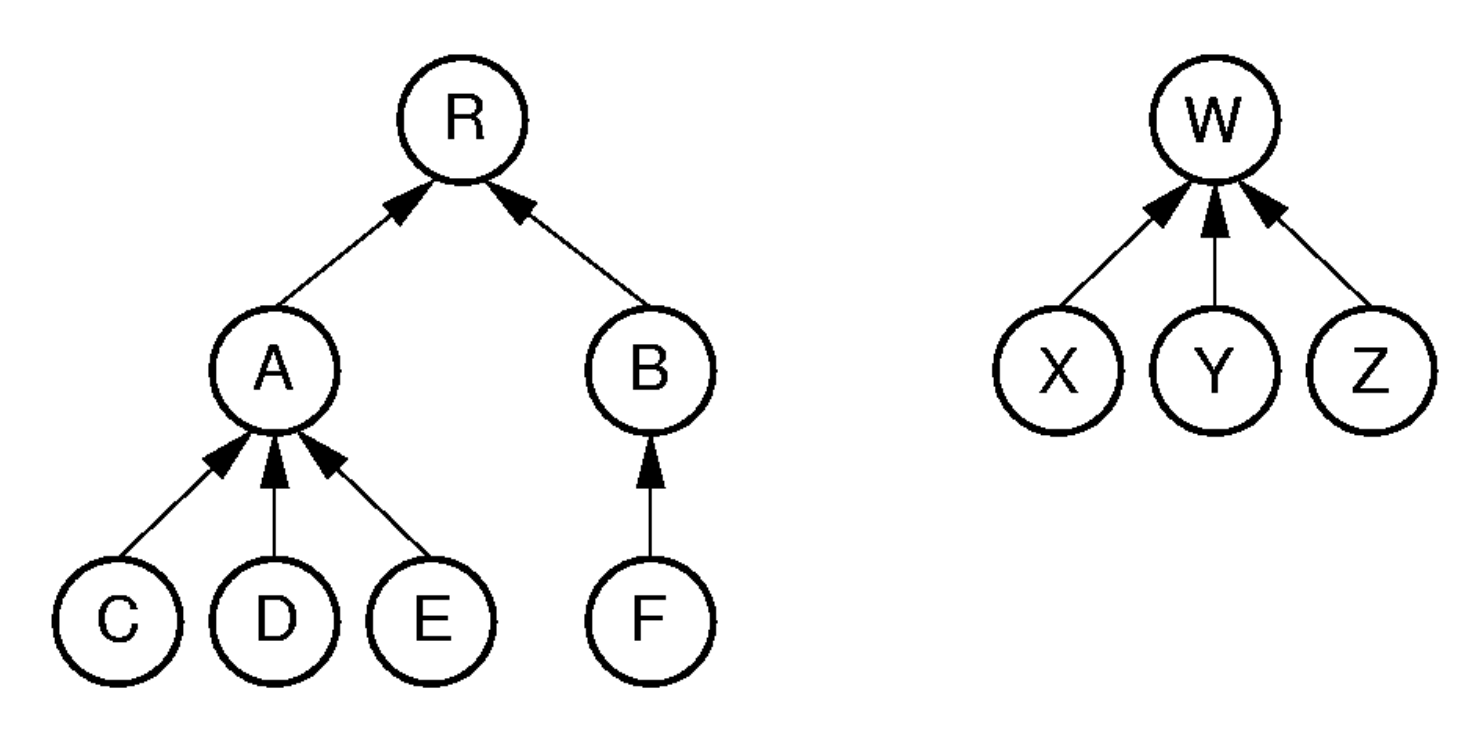
Non-Binary Trees

Posted Jun 14, 2025

By Jaebaek Lee

12 min read

Non-Binary Trees

Non-Binary Trees는 각 노드가 두 개 이상의 자식을 가질 수 있는 트리 구조

ADT

  
interface GTNode<E>{
    public E value();
    public boolean isLeaf();
    public GTNode<E> parent();
    public GTNode<E> leftmostChild();
    public GTNode<E> rightSibling();
    public void setValue(E value);
    public void setParent(GTNode<E> parent);
    public void insertFirst(GTNode<E> child);
    public void insertNext(GTNode<E> child);
    public void removeFirst();
    public void removeNext();
}

value()는 노드의 값을 반환
isLeaf()는 노드가 리프 노드인지 확인
parent()는 부모 노드를 반환
leftmostChild()는 가장 왼쪽 자식 노드를 반환
rightSibling()는 오른쪽 형제 노드를 반환
setValue(E value)는 노드의 값을 설정
setParent(GTNode<E> parent)는 부모 노드를 설정
insertFirst(GTNode<E> child)는 첫 번째 자식 노드를 삽입
insertNext(GTNode<E> child)는 다음 형제 노드를 삽입
removeFirst()는 첫 번째 자식 노드를 제거
removeNext()는 다음 형제 노드를 제거
이 ADT는 Non-Binary Tree의 기본적인 연산을 정의하며, 각 노드가 여러 자식을 가질 수 있도록 설계됨.

Traversal

Binary Tree에서는 Preorder, Inorder, Postorder가 정의됨
Non-Binary Tree에서는 Preorder, Postorder만 정의됨
- Inorder는 왼쪽 자식을 순회하고, 현재 노드를 방문하고, 오른쪽 자식을 순회하는 방식인데, Non-Binary Tree에서는 왼쪽 자식과 오른쪽 자식을 구분할 수 없으므로 정의되지 않음

Preorder Traversal

  
static <E> void preorder(GTNode<E> root) {
  PrintNode(root);
  if (!root.isLeaf()) {
      GTNode<E> child = root.leftmostChild();
      while (child != null) {
          preorder(child);
          child = child.rightSibling();
      }
  }
}

Postorder Traversal

  
static <E> void postorder(GTNode<E> root) {
  if (!root.isLeaf()) {
      GTNode<E> child = root.leftmostChild();
      while (child != null) {
          postorder(child);
          child = child.rightSibling();
      }
  }
  PrintNode(root);
}

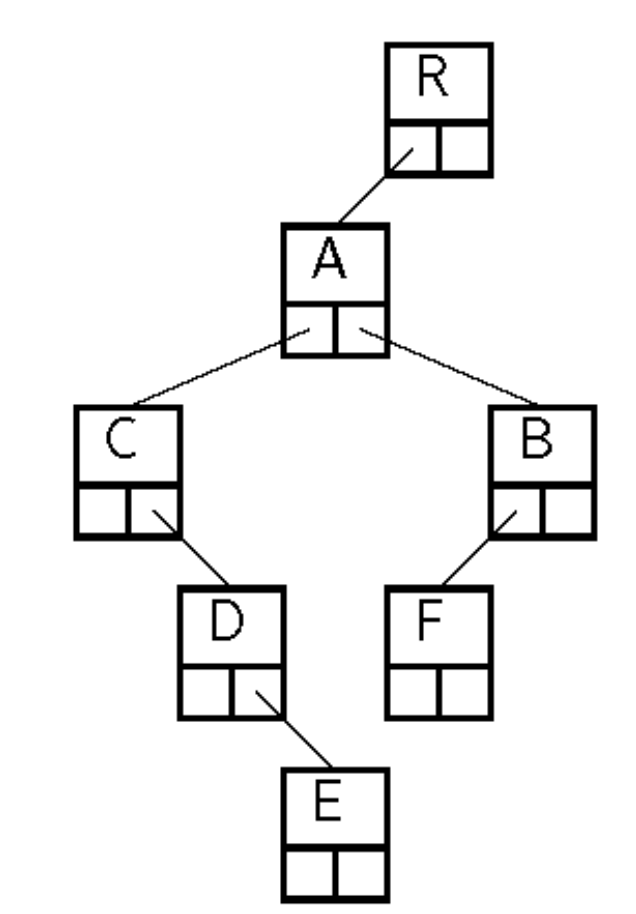
Parent Pointer Implementation

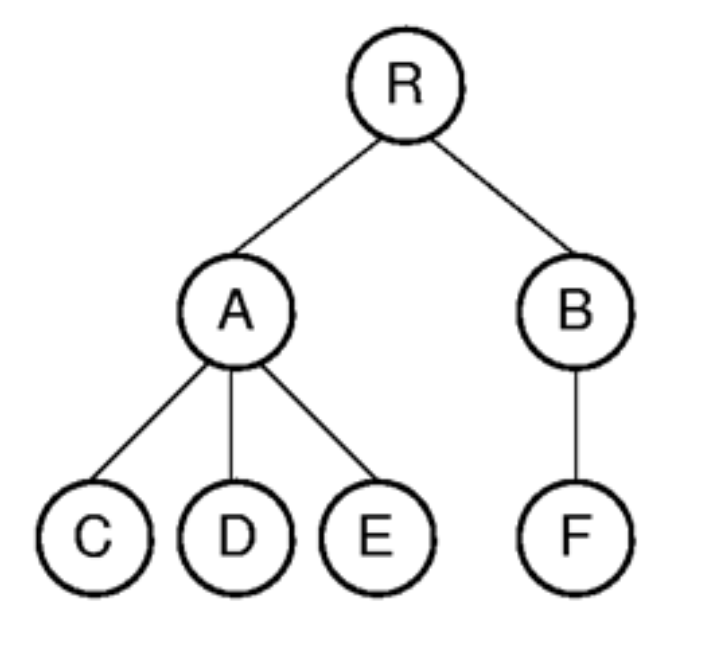
Non-Binary Tree를 구현할 때, 각 노드가 부모 노드를 가리키는 포인터를 추가하여 구현할 수 있음

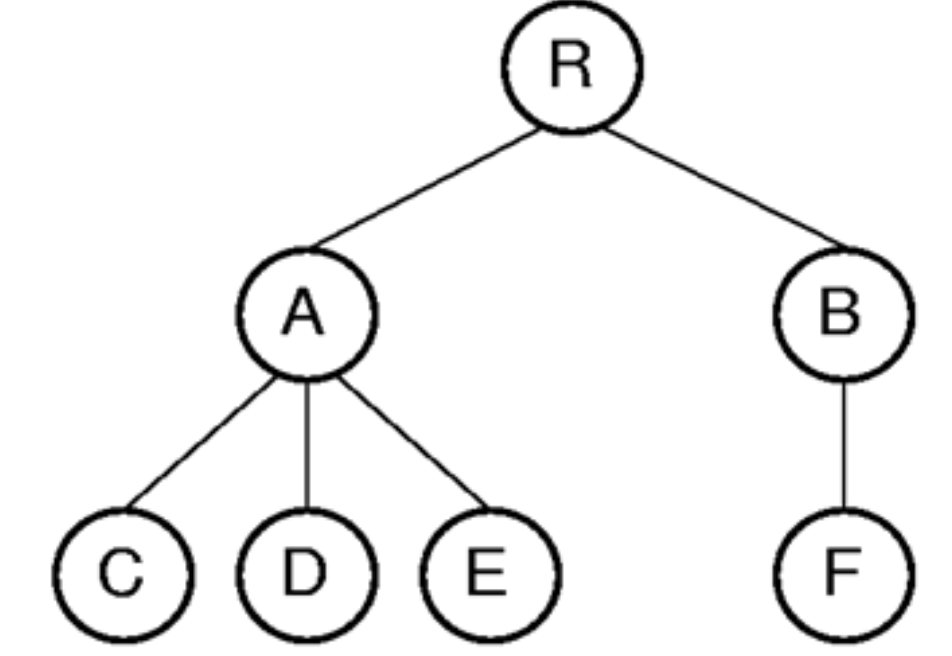
위 이미지에 대해, Parent Pointer Implementation을 적용한 결과는 다음과 같음

Parent’s Index	Label	Node’s Index
Null	R	0
0	A	1
0	B	2
1	C	3
1	D	4
1	E	5
2	F	6
Null	W	7
7	X	8
7	Y	9
7	Z	10

이 구현에서는 각 노드가 부모 노드를 가리키는 포인터를 추가하여, 트리 구조를 표현함
서로 다른 두 노드가 한 트리 안에 속하는지의 여부를 쉽게 확인할 수 있음

  
public boolean differ(int a, int b) {
    Integer root1 = FIND(a);
    Integer root2 = FIND(b);
    return root1 != root2;
}
public Integer FIND(Integer x) {
    if (parent[x] == null) {
        return x;
    } 
    while (parent[x] != null) {
        x = parent[x];
    }
    return x;
}

Union-Find

Union-Find는 두 집합의 비교에 중요하게 사용되는 연산
- Union: 두 집합을 합치는 연산
- Find: 두 원소가 같은 집합에 속하는지 확인하는 연산

Implementation

Naive Implementation
- Union: $A \cup B$의 모든 원소에 대해 $id(i)$(객체 i가 속한 집합의 대표 원소)를 업데이트, $O(n)$
- Find: $id(i)$를 반환, $O(1)$
Parent Pointer Implementation
- Union: $A$와 $B$의 root를 찾아서, 한 집합의 root를 다른 집합의 root로 설정, $O(FIND)$
- Find: $id(i)$를 찾을 떄, 부모 루트를 타고 거슬러 올라가면서 찾음, $O(\log n)$
  - Path Compression
    - Find 연산을 수행할 때, 경로 상의 모든 노드의 부모를 root로 설정하여, 다음 Find 연산에서 더 빠르게 찾을 수 있도록 함
    - $O(\log n)$에서 $O(1)$로 최적화됨
Union

  
public void union(int a, int b) {
    Integer rootA = FIND(a);
    Integer rootB = FIND(b);
    if (rootA != rootB) {
        parent[rootB] = rootA; // rootB의 부모를 rootA로 설정
    }
}

이때, 두 집합(트리)를 합칠 때, 더 작은 트리를 더 큰 트리의 자식으로 설정하는 것이 효율적임. FIND 연산 등을 수행할 때, 트리의 높이를 최소화하여 탐색 시간을 줄일 수 있기 때문임.

Weighted union rule
- Union 연산을 수행할 때, 두 트리의 크기를 비교하여 더 작은 트리를 더 큰 트리의 자식으로 설정하는 방법
- 이 방법은 트리의 높이를 최소화하여, 최대 $\log n$의 높이를 유지하게 함
증명
- 가정:
  - 초기에는 각 노드가 하나의 독립적인 트리 → 높이 0
  - n 개의 노드 → n 개의 트리
- 어떤 노드 $v$가 속한 트리 $A$의 높이를 $h$라고 할 때, $h$가 증가하기 위해선 $A$가 더 큰 트리로 합쳐져야 함
- 이때 합쳐진 트리의 크기는 $ A $의 최소 두 배 이상이 되어야 함
  - $ A \leq B $인 트리 $B$와 합쳐질 때, $ A \cup B = A + B \geq 2 A $
- 따라서, 트리의 높이가 증가할 때마다 트리의 크기는 최소 두 배 이상 증가하게 됨
- 노드 $v$는 처음에 자기 자신만을 포함하는 트리로 시작하므로, 높이가 $0$일 때 트리의 크기는 $1$이 됨
- 깊이가 늘어날 때마다 트리의 크기는 최소 두 배 이상 증가하게 되므로, 최종 트리 $ T $의 크기는 $ T \geq 2^h$가 됨
- 그런데 트리의 크기는 $n$이므로, $ T \leq n$이 됨
- 따라서, $2^h \leq n$, 즉 $h \leq \log_2 n$이 성립함
Path Compression(Find)
- Find 연산을 수행할 때, 경로 상의 모든 노드의 부모를 root로 설정하여, 다음 Find 연산에서 더 빠르게 찾을 수 있도록 함

  
public Integer FIND(Integer x) {
    if (parent[x] == null) {
        return x;
    }
    parent[x] = FIND(parent[x]); // 경로 상의 모든 노드의 부모를 root로 설정
    return parent[x];
}

General Tree Implementation

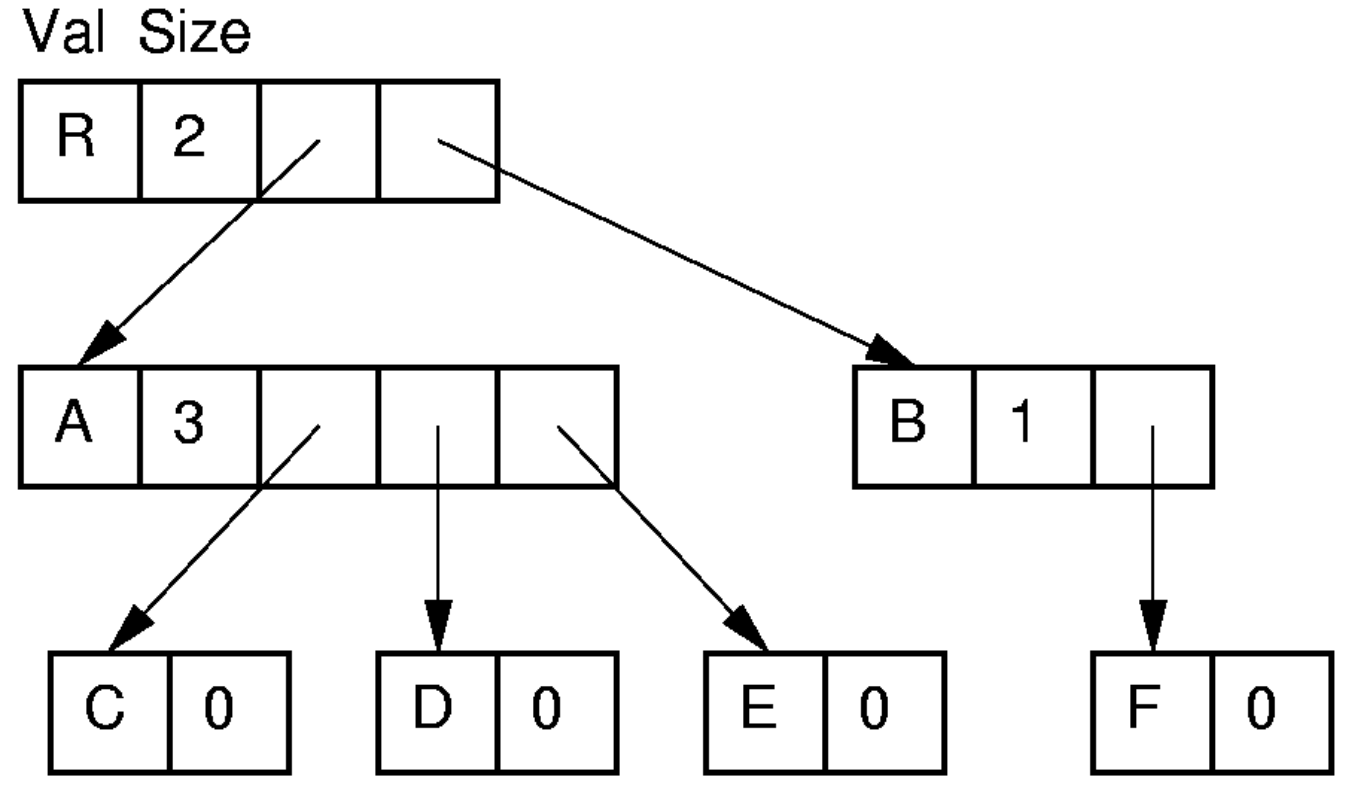
List of Children

각 노드가 자식 노드의 리스트를 가지고 있는 방식
예:

Index	Value	Parent	Children
0	R	-	[1, 3]
1	A	0	[2, 4, 6]
2	C	1	[]
3	B	0	[5]
4	D	1	[]
5	F	3	[]
6	E	1	[]

Pros
- parent(), leftmostChild() 연산이 $O(1)$로 빠름
- 두 트리가 같은 array에 있다면, UNION 연산이 효율적
  - 합쳐지는 트리의 루트 노드에 parent를 설정하고, 자식 리스트에 단순히 추가하는 방식으로 구현 가능
Cons
- rightSibling() 연산이 $O(n)$으로 느림
- linked list가 아닌 array-based로 구현할 경우, 노드의 개수를 미리 알아야함

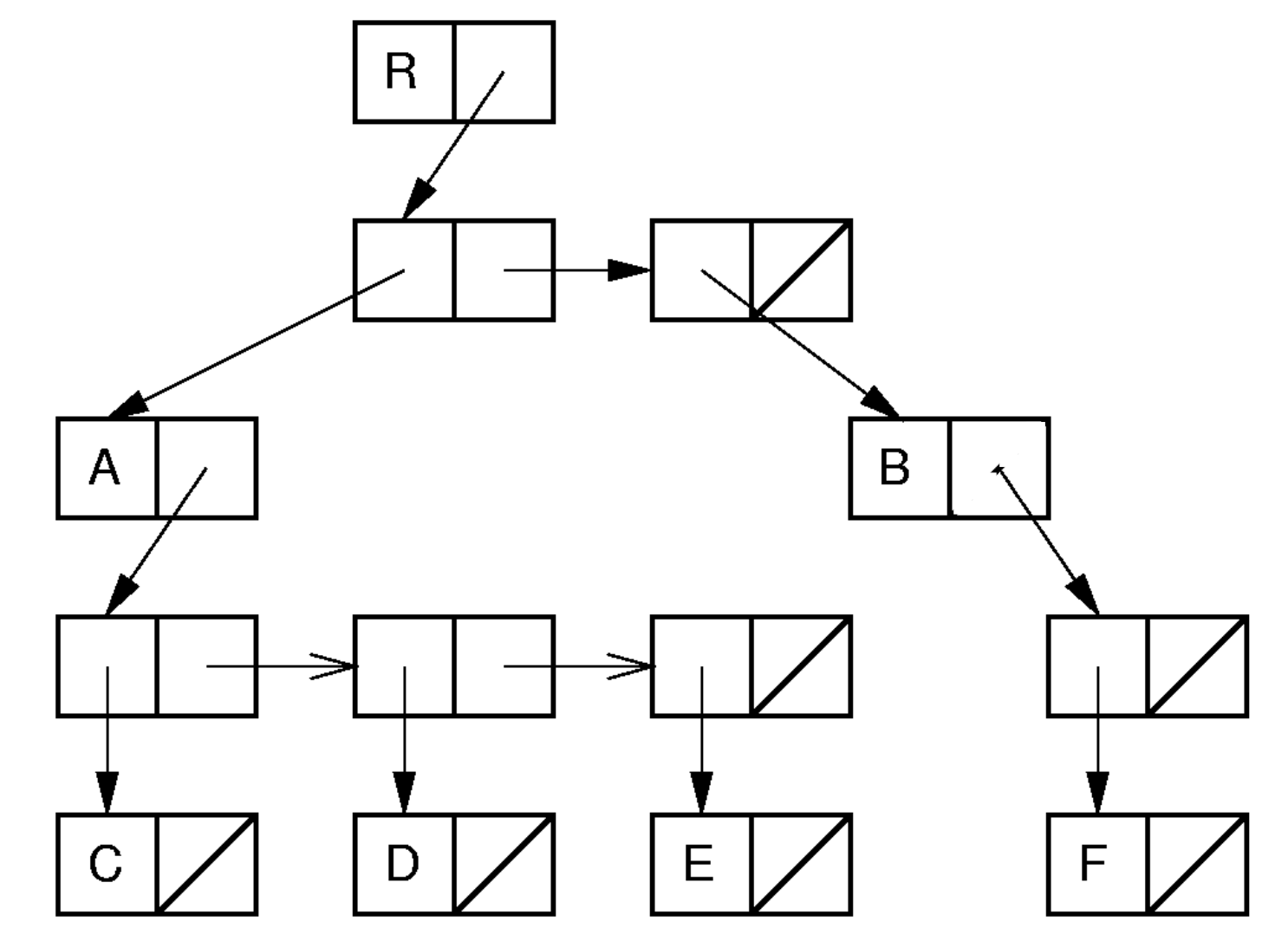
Leftmost Child/Right Sibling

각 노드가 왼쪽 자식과 오른쪽 형제 노드를 가리키는 포인터를 가지고 있는 방식
예:

Index	Value	Parent	Leftmost Child	Right Sibling
0	R	-	1	-
1	A	0	3	2
2	B	0	6	-
3	C	1	-	4
4	D	1	-	5
5	E	1	-	-
6	F	2	-	-

Pros
- parent(), leftmostChild(), rightSibling() 연산이 $O(1)$로 빠름
- list of children 방식에서는 각 노드마다 자식 리스트를 관리해야 했지만, 이 방식에서는 자식 개수에 상관없이 각 노드가 두 개의 포인터(leftmostChild, rightSibling)만을 관리하므로, 메모리 사용이 효율적
Cons
- array-based로 구현할 경우, 노드의 개수를 미리 알아야함

Dynamic Node

ver-1: List of Children의 Linked List 방식

Pros
- parent(), leftmostChild() 연산이 $O(1)$로 빠름
- 두 트리의 결합이 효율적
  - 합쳐지는 트리의 루트 노드에 parent를 설정하고, 자식 리스트에 단순히 추가하는 방식으로 구현 가능
- 미리 노드의 개수를 알 필요 없음
Cons
- rightSibling() 연산이 $O(n)$으로 느림
- 링크 기반이지만, 자식들을 관리하기 위해 내부적으로 fixed-size array 또는 reallocable array가 필요

ver-2:

이 방식에서는 각 노드가 leftmostChild 포인터, rightSibling 포인터를 자식 수에 상관없이 고정 크기를 가짐
ver1과 비교해 유연하지만, 더 많은 공간 요구

Dynamic Left-Chid/Right-Sibling

Non-binary tree를 binary tree처럼 변환해, leftmostChild는 왼쪽 포인터, rightSibling는 오른쪽 자식 포인터로 저장
기존 Left-Chid/Right-Sibling과 비교해 pre-allocate 메모리 필요 없음
기존 ver-2와 비교해 더 적은 공간을 씀

Sequential Implementations

연산과는 상관 없이, 트리 구조의 공간을 최소화하는 방법이 필요할 때도 있음
- 트리를 저장할때는 연산을 고려할 필요가 없음
Sequential Implementations는 트리 저장에 최소한의 공간을 사용하는 방법론
- 트리의 노드들을 pre-order로 순회하여, 노드의 값을 배열에 저장
- pointer 저장 필요 없음

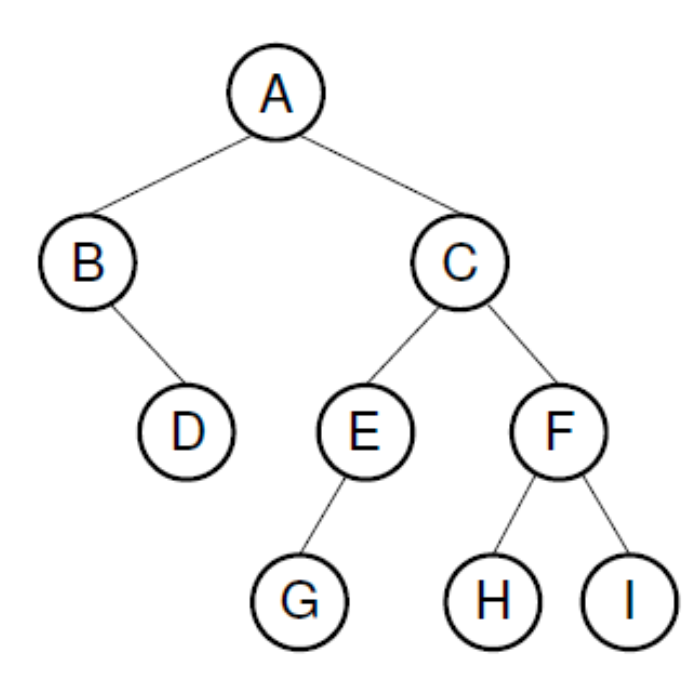
For Binary Trees

Null pointer를 /로 표시
- AB/D//CEG///FH//I//
- 각 /는 왼쪽 자식 혹은 오른쪽 자식이 없음을 나타냄
- 각 노드 외에도 /를 추가로 저장함으로써 저장되는 overhead가 발생함
- sparse한 트리에서는 공간 낭비가 심함
Internal Node를 bit로 표시
- 노드 값 옆에 '를 붙여서 Internal Node를 표시
- Full binary tree에서는 null pointer 기호 필요없음
- A'B'/DC'E'/G//F'H//I//
- Space Overhead: 각 Internal Node마다 1 bit를 추가로 저장

For Non-Binary(General) Trees

Non-Binary Tree Sequential Implementation

Pre-order로 순회하여, 노드의 값을 배열에 저장
각 subtree의 마지막에 )를 추가하여, 각 subtree의 끝을 표시
RAC)D)E))BF)))

해당 포스트는 서울대학교 컴퓨터공학부 강유 교수님의 자료구조 25-1학기 강의를 정리한 내용입니다.

자료구조

This post is licensed under CC BY 4.0 by the author.

Non-Binary Trees

ADT

Traversal

Parent Pointer Implementation

Union-Find

Implementation

General Tree Implementation

List of Children

Leftmost Child/Right Sibling

Dynamic Node

Dynamic Left-Chid/Right-Sibling

Sequential Implementations

For Binary Trees

For Non-Binary(General) Trees

Trending Tags