PCA & Eigenface
PCA
어떤 고차원의 정보를 저차원으로 압축할 때, 가장 정보를 잘 보존하는 방법은 무엇일까?
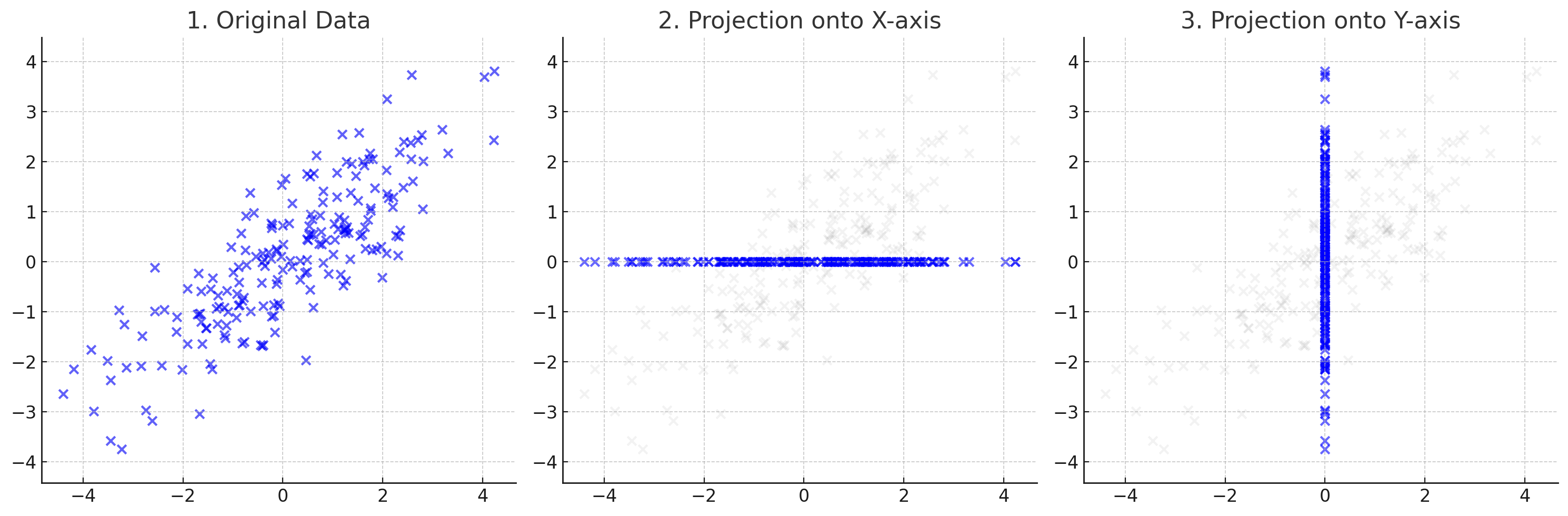
위 그림은 2차원 데이터를 각각 x축과 y축으로 압축한 것이다. 하지만, 이와 같은 압축이 최적이라고 말하긴 어렵다. 압축했을때의 정보 손실, 즉 각 축에서 데이터포인트까지의 거리를 최소화할 때, 원래 데이터의 정보를 잘 보존한다고 할 수 있다.
PCA(Principal Component Analysis) 는 이러한 압축을 수행하는 방법 중 하나로, 데이터의 분산을 최대화하는 방향을 축으로하여 저차원으로 압축하는 방법이다.
PCA는 데이터의 분산을 최대화하는 방향을 찾기 위해, 공분산 행렬을 계산하고, 이 행렬의 고유벡터를 구하여 새로운 축을 정의한다.
이와 같은 방법으로 분산을 최대화할 수 있는 이유는 다음과 같다:
주어진 데이터가 $u$방향으로 projection 되었을 때, 가장 큰 분산을 갖도록 하는 $u$를 찾도록 해야한다.(평균이 0이라고 가정)
주어진 데이터 $x_i$에 대해, $u$방향으로 projection된 값은 $u^T x_i$이다.
이때, $u$방향으로 projection 되었을 때의 분산은 다음과 같이 표현할 수 있다.
- 위 식에서 $u^T x_i$는 $x_i$를 $u$방향으로 projection한 스칼라 값이다.
- 위 식은 해당 값의 제곱을 평균한 값으로, 평균이 0이라고 가정했으므로, 분산을 의미한다.
- 위 식을 다음과 같이 변형할 수 있다.
위 식에서 $C = \frac{1}{M}\sum_{i=1}^M x_i x_i^T$는 공분산 행렬이다.
따라서, $u$방향으로 projection 되었을 때의 분산은 $u^T C u$로 표현할 수 있다.
따라서 $u$를 찾는 문제는 $u^T C u$를 최대화하는 $u$를 찾는 문제로 변환할 수 있다.
이때, $u$는 단위 벡터이므로, $ u ^2 = 1$이라는 제약조건을 추가할 수 있다. - 따라서, $u$를 찾는 문제는 다음과 같이 표현할 수 있다.
- 위 문제는 Lagrange multiplier를 사용하여 다음과 같이 변형할 수 있다.
- 위 식을 정리하면 다음과 같다.
- 위 식은 고유값 문제로, $C$의 고유값 $\lambda$와 고유벡터 $u$를 찾는 문제로 변환할 수 있다.
- 따라서, 공분산 행렬 $C$의 고유값과 고유벡터를 구하면, 투영시 분산을 최대화 하는 축을 찾을 수 있다.
Dimensionality Reduction
위 사례에서는 한개의 축(가장 큰 고유값에 해당하는 고유벡터)만을 사용하여 저차원으로 압축하였다. 하지만, PCA는 고차원의 정보를 원하는 만큼 축을 선택하여 해당 차원으로 압축할 수 있다.
예를 틀어 $m$차원의 데이터 $x_i \in \mathbb{R^m}$에 대해 $n$차원 정보로 압축하고 싶다면, 공분산 행렬 $C$의 고유값을 내림차순으로 정렬하여 $n$개의 고유벡터를 선택하면 된다.
\[y_i = \begin{bmatrix} u_1^T x_i \\ u_2^T x_i \\ \vdots \\ u_n^T x_i \end{bmatrix} \in \mathbb{R^n}\]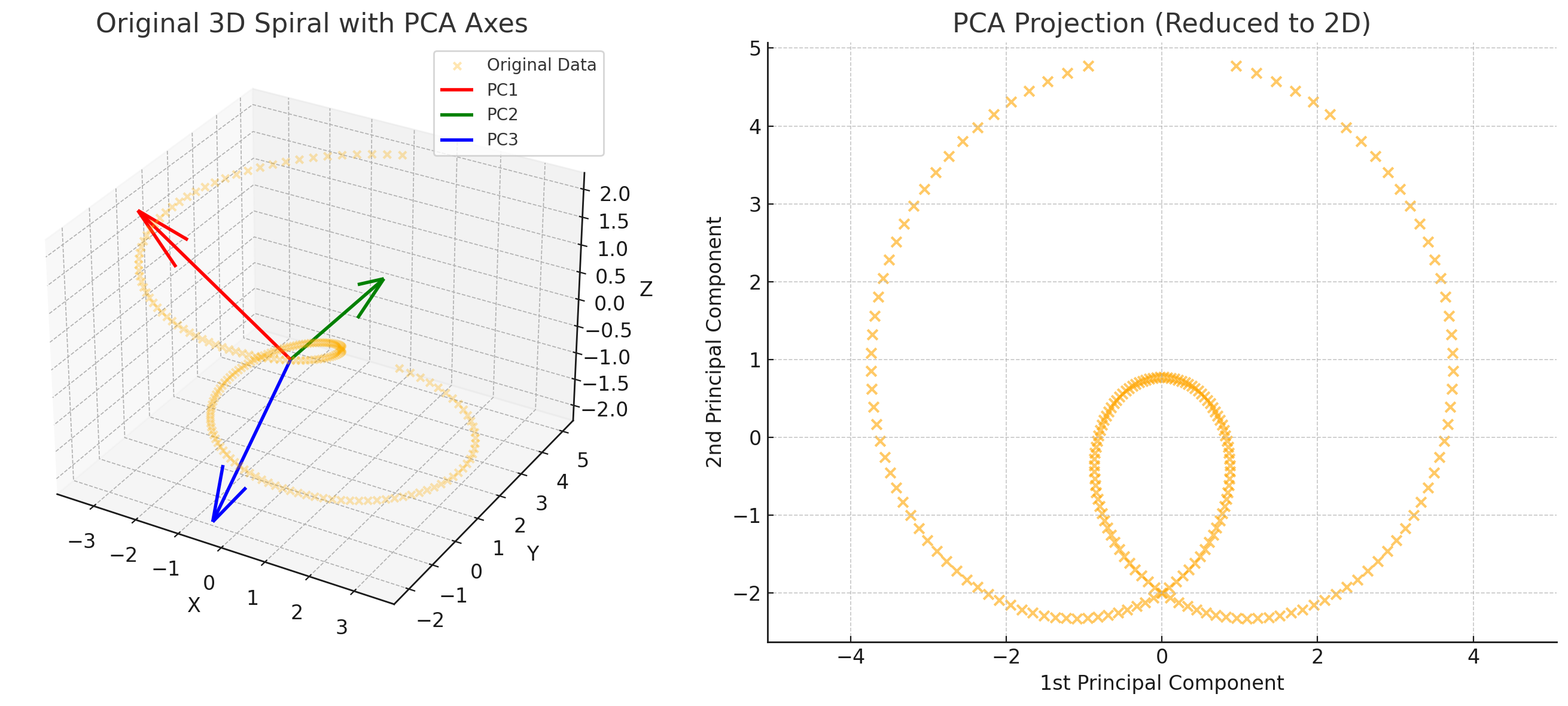
PCA as SVD
위 과정에서 “주성분” $u_i$를 찾기 위해 공분산 행렬 $C$의 고유값을 구하는 방법을 사용하였다. 이때, 공분산 행렬 $C$는 $\frac{1}{M} X^T X$로 표현된다. 이는 scaling factor $1/M$을 제외하면, $X^T X$와 같다. 따라서 지금껏 수행한 PCA는 $X^T X$의 고유값과 고유벡터를 구하는 과정과 같다.
따라서, PCA는 SVD(Singular Value Decomposition)로도 표현할 수 있다.
\[X = U \Sigma V^T\]- $X$: $n$차원의 데이터 $M$개로 구성된 $n \times M$ 행렬
- $U$: $X^T X$(공분산)의 고유벡터로 구성된 $n \times n$ 직교행렬
- $\Sigma$: $X^T X$의 고유값으로 구성된 $n \times M$ 대각행렬
- $V$: $X X^T$의 고유벡터로 구성된 $M \times M$ 직교행렬
이때, $k$개의 주성분으로 데이터를 압축하는 것은, $U$, $\Sigma$, $V$의 앞 $k$개 행렬을 선택하여 $X$를 근사하는 것이다.
\[X \approx U_k \Sigma_k V_k^T\]이때, $\Sigma_k V_k^T$의 열벡터는 각각 $x_i$가 k개의 주성분으로 표현된($y_i = U^T x_i$) 값이다. 즉, $y_i$는 $x_i$를 $k$개의 주성분으로 표현한 값이다.
원본 데이터 $x_i$를 거꾸로 $U_k$의 $k$개의 주성분으로 표현할 수도 있다.
\[x_i \approx y_i^1 u_1 + y_i^2 u_2 + \cdots + y_i^k u_k\]- $y_i^j$: $y_i$의 $j$번째 원소
즉 압축된 데이터 $y_i$의 원소를 계수로 주성분 $u_1, u_2, \cdots, u_k$를 선형결합하여 원본 데이터 $x_i$를 근사할 수 있다.
Eigenface
Eigenface는 PCA를 사용하여 얼굴 이미지를 압축하고, 얼굴 인식에 활용하는 방법이다.
앞서 살펴본 PCA는 원본 데이터 정보를 최대한 그 특징을 보존하면서 저차원으로 압축하는 방법이다.
인간의 얼굴 역시 고차원 정보를 갖고 있지만, 공통적인 패턴을 갖고 있고, 이 패턴을 PCA를 사용해 저차원 정보로 압축한다면 특징을 보존하면서 저차원으로 압축할 수 있다.
Procedure
Eigenface는 다음과 같은 과정을 거쳐 얼굴 이미지를 압축한다.
- 얼굴 이미지 데이터셋을 준비한다.
- 얼굴 이미지의 평균을 계산한다.
- 각 얼굴 이미지에서 평균을 빼준다.
- 각 얼굴 이미지에 대해 공분산 행렬을 계산한다.
- 공분산 행렬의 고유값과 고유벡터를 구한다.
- $k$개의 고유벡터($u_1, u_2, \cdots, u_k$)를 선택한다.
이제 각 얼굴은 다음과 같이 근사될 수 있다.
\[x_i \approx \bar{x} + \sum_{j=1}^k \alpha_i^j u_j\]- $x_i$: $i$번째 얼굴 이미지
- $\bar{x}$: 얼굴 이미지의 평균
- $u_j$: $j$번째 주성분
- $\alpha_i^j$: $u_j^T(x_i - \bar{x})$로, 주성분 $u_j$에 대한 $x_i$의 계수
각 eigenface $u_j$는 얼굴 이미지의 주성분을 나타내며, 각 얼굴 이미지는 이 주성분을 선형 결합하여 근사할 수 있다. 해당 값에 대응되는 이미지는 흐릿한 얼굴 모양의 패턴 이미지로 나타난다.

How to Recognize
Eigenface를 사용하여 얼굴을 인식하는 방법은 다음과 같다.
- 학습
- 얼굴 이미지 데이터셋을 준비한다.
- 평균 얼굴 및 주성분(eigenface)을 계산한다.
- 각 얼굴 이미지 $x_i$를 주성분으로 투영하고, 특징벡터($\alpha_i$)를 저장한다.
- 인식
- 인식할 얼굴 이미지 $x$를 준비한다.
- 평균 얼굴을 빼준다.
- 주성분으로 투영하고, 특징벡터($\alpha_{test}$)를 계산한다.
- 학습된 특징벡터($\alpha_i$)와 인식된 특징벡터($\alpha_{test}$) 간의 거리를 계산한다.
- 가장 가까운 특징벡터를 갖는 얼굴 이미지를 인식 결과로 선택한다.
해당 포스트는 서울대학교 컴퓨터공학부 주한별 교수님의 컴퓨터비전 25-1학기 강의를 정리한 내용입니다.