Recommender Systems

Posted Jun 1, 2025

By Jaebaek Lee

43 min read

Recommender Systems

추천 시스템(Recommender Systems)은 데이터를 기반으로 사용자에게 개인화된 추천을 제공하는 시스템이다.

Goal of Recommender Systems:
- Relevance: 사용자에게 적합한 아이템을 추천하는 것.
- Novelty: 사용자에게 새로운 아이템을 추천하는 것.
- Serendipity: 예상치 못한 유용한 아이템을 추천하는 것.
- Diversity: 다양한 아이템을 추천하는 것.
- Explanation: 추천 이유를 설명하는 것.
Versions of Recommender Systems:
- Prediction version: 사용자-아이템 간의 평점 예측.
- Ranking version: 사용자에게 아이템을 순위별로 추천.
- 예측 버전이 보다 일반적이고 유연성이 높다.
Basic Models of RS:
- Data
  - User-Item Interaction: 사용자와 아이템 간의 상호작용 데이터.
  - Attribute Data: 사용자와 아이템의 속성 데이터.(예: 사용자 프로필, 아이템 설명 등)
- Modeling
  - Collaborative Filtering: 사용자와 아이템 간의 상호작용을 기반으로 추천.
  - Content-Based Filtering: 아이템의 속성을 기반으로 추천.
  - Hybrid Methods: Collaborative Filtering과 Content-Based Filtering을 결합한 방법.
  - Hybrid: 사용자와 아이템의 속성을 모두 활용하여 추천하는 방법.

Collaborative Filtering

Collaborative Filtering은 사용자와 아이템 간의 상호작용 데이터를 기반으로 추천을 생성하는 방법이다.

이웃 기반 예측:
- 가정: 유사한 사용자 혹은 아이템은 유사한 선호도를 가진다.
- Nearest Neighbors 개념과 유사.

Memory-Based CF

Memory-Based Collaborative Filtering은 사용자와 아이템 간의 상호작용 데이터를 직접 활용하여 추천을 생성하는 방법이다.

User-Based CF:
- 유사한 사용자들을 찾아서 추천을 생성.
- 예: 사용자 A와 유사한 사용자 B가 높은 평점을 준 아이템을 A에게 추천.
Item-Based CF:
- 아이템 간의 유사성을 기반으로 추천을 생성.
- 예: 아이템 X와 유사한 아이템 Y가 높은 평점을 받은 경우, X를 좋아하는 사용자에게 Y를 추천.
Limitations of Memory-Based CF:
- Scalability: 사용자와 아이템의 수가 많아질수록 계산 비용이 증가.
- Sparsity: 사용자-아이템 상호작용 데이터가 희소할 경우 추천의 품질 저하.
- Cold Start Problem: 새로운 사용자나 아이템에 대한 추천이 어려움.
일반적으로 item-based CF가 user-based CF보다 더 효과적이다.

User-based CF

Formulation:
- $m$: 사용자 수
- $n$: 아이템 수
- $R \in \mathbb{R}^{m \times n}$: 사용자-아이템 평점 행렬
문제 유형:
- 평점 예측:
  - 사용자 $u$가 아이템 $i$에 부여할 평점 $\hat{r}_{ui}$ 예측.
- Top-K 추천:
  - 사용자 $u$에게 가장 적합한 K개의 아이템 추천.
  - 아이템 $j$에 대해 가장 적합한 K명의 사용자 추천.

데이터 준비:
- $I_u$: 사용자 $u$가 평가한 아이템 집합.
- $\mu_u$: 사용자 $u$의 평균 평점.
  $\mu_u = \frac{1}{|I_u|} \sum_{k \in I_u} r_{uk}$
사용자 간 유사도 계산:
- 피어슨 상관계수를 사용하여 사용자 간의 유사도 계산.
- 사용자 $u$와 $v$ 간의 유사도는 다음과 같이 정의된다. $Sim(u, v) = \frac{\sum_{k \in I_u \cap I_v} (r_{uk} - \mu_u)(r_{vk} - \mu_v)}{\sqrt{\sum_{k \in I_u \cap I_v} (r_{uk} - \mu_u)^2} \sqrt{\sum_{k \in I_u \cap I_v} (r_{vk} - \mu_v)^2}}$
중심화된 평점 계산:

\[s_{ui} = r_{ui} - \mu_u\]

최근접 이웃 사용자 선택:
- $P_u(j)$: target 사용자 $u$에게 가장 유사한 사용자 중 item $j$를 평가한 사용자 집합.
예측 평점 계산:
$\hat{r}_{uj} = \mu_u + \frac{\sum_{v \in P_u(j)} Sim(u, v) (r_{vj}-\mu_v)}{\sum_{v \in P_u(j)} |Sim(u, v)|}= \mu_u + \frac{\sum_{v \in P_u(j)} Sim(u, v) s_{vj}}{\sum_{v \in P_u(j)} |Sim(u, v)|}$

Example Dataset:

User	Item 1	Item 2	Item 3	Item 4	Item 5	Item 6	Mean Rating	Cosine(i,3)	Pearson(i,3)
User 1	7	6	7	4	5	4	5.5	0.956	0.894
User 2	6	7	?	4	3	4	4.8	0.981	0.939
User 3	?	3	3	1	1	?	2.0	1.000	1.000
User 4	1	2	2	3	3	4	2.5	0.789	-1.000
User 5	1	?	1	2	3	3	2.0	0.645	-0.817

target user: User 3
target item: Item 1, Item 6
Top-2 Nearest Neighbors: User 1, User 2
예측 평점 계산:
- Item 1:
  $\hat{r}_{31} = \mu_3 + \frac{Sim(3, 1) s_{11} + Sim(3, 2) s_{21}}{|Sim(3, 1)| + |Sim(3, 2)|} = 2.0 + \frac{0.894 \cdot 7 + 0.939 \cdot 6}{|0.894| + |0.939|} \approx 6.49$
  - Mean-Centered Rating:
    $\hat{r}_{31} = 2 + \frac{0.894 (7 - 5.5) + 0.939 (6 - 4.8)}{0.894 + 0.939} \approx 3.35$
- Item 6:
  $\hat{r}_{36} = \mu_3 + \frac{Sim(3, 1) s_{16} + Sim(3, 2) s_{26}}{|Sim(3, 1)| + |Sim(3, 2)|} = 2.0 + \frac{0.894 \cdot 4 + 0.939 \cdot 4}{|0.894| + |0.939|} = 4$
  - Mean-Centered Rating: $\hat{r}_{36} = 2 + \frac{0.894 (4 - 5.5) + 0.939 (4 - 4.8)}{0.894 + 0.939} \approx 0.86$
Variations in Filtering Peer Groups
- Top-K 사용자를 고를 때, 타겟 사용자와 약하거나 음의 상관관계를 가진 사용자도 포함할 수 있다.
- 이로 인해 부정확한 추천이 발생할 수 있으므로, 약하거나 음의 상관관계를 가진 사용자를 제외하는 것이 일반적이다.

Item-based CF

유사한 아이템을 기반으로 추천을 생성하는 방법
사용자 간의 유사도를 계산하는 것이 아니라, 아이템 간의 유사도를 계산하여 추천을 생성한다.
각 사용자 row의 rating은 0을 기준으로 중심화된 평점으로 변환한다.
유사도는 Adjusted Cosine Similarity를 사용.
수식:
$AdjustedCosine(i, j) = \frac{\sum_{u \in U_i \cap U_j} (r_{ui} - \mu_u)(r_{uj} - \mu_u)}{\sqrt{\sum_{u \in U_i \cap U_j} (r_{ui} - \mu_u)^2} \sqrt{\sum_{u \in U_i \cap U_j} (r_{uj} - \mu_u)^2}}$
- $U_i$: 아이템 $i$를 평가한 사용자 집합
예측 평점 계산:
$\hat{r}_{ut} = \frac{\sum_{j \in Q_t(u)} AdjustedCosine(j, t) \cdot (r_{uj})}{\sum_{j \in Q_t(u)} |AdjustedCosine(j, t)|} + \mu_u$
- $Q_t(u)$: 사용자 $u$가 평가한 아이템 집합 중 아이템 $t$와 유사한 top-K 아이템 집합
즉, 사용자 $u$ 자신의 기존 평점과 아이템 간의 유사도를 결합해 예측 수행
Example Dataset:
Mean-centered Ratings:

User-Id ↓ / Item-Id ⇒	1	2	3	4	5	6
1	1.5	0.5	1.5	-1.5	-0.5	-1.5
2	1.2	2.2	?	-0.8	-1.8	-0.8
3	?	1	1	-1	-1	?
4	-1.5	-0.5	-0.5	0.5	0.5	1.5
5	-1	?	-1	0	1	1

Target User: User 3
Target Item: Item 1, Item 6
Cosine Similarity:

기준 아이템 → / 비교 아이템 ↓	1	2	3	4	5	6
Cosine(1, j)	1.000	0.735	0.912	-0.848	-0.813	-0.990
Cosine(6, j)	-0.990	-0.622	-0.912	0.829	0.730	1.000

Top-2 Nearest Neighbors:
- Item 1: Item 3, Item 2
- Item 6: Item 4, Item 5
예측 평점 계산:
- Item 1:
  $\hat{r}_{31} = \frac{AdjustedCosine(1, 2) \cdot r_{32} + AdjustedCosine(1, 3) \cdot r_{33}}{|AdjustedCosine(1, 2)| + |AdjustedCosine(1, 3)|} + \mu_3 = \frac{0.735 \cdot 1 + 0.912 \cdot 1}{|0.735| + |0.912|} + 2 = 3$
- Item 6: $\hat{r}_{36} = \frac{AdjustedCosine(6, 4) \cdot r_{34} + AdjustedCosine(6, 5) \cdot r_{35}}{|AdjustedCosine(6, 4)| + |AdjustedCosine(6, 5)|} + \mu_3 = \frac{0.829 \cdot -1 + 0.730 \cdot -1}{|0.829| + |0.730|} + 2 = 1$

Implementation Issues

Offline Phase
- user-user, item-item 유사도 계산
- 각 사용자/아이템별 peer-group 계산
Online Phase
- 저장된 유사도와 peer-group을 활용하여 예측 평점 계산
Computational Complexity of Offline Phase:
- $n’$: 사용자 한명이 평가한 아이템 수
- $m’$: 아이템 하나가 받은 평가 수
- 시간 복잡도:
  - User-Based CF
    - 특정 사용자 $u$에 대해 peer-group 계산: $O(mn’)$
      이 사용자가 평가한 아이템 $n’$개에 대해 모든 다른 사용자와의 유사도 계산
    - 모든 사용자에 대해 peer-group 계산: $O(m^2 n’)$
      위 작업을 모든 사용자 쌍에 대해 유사도 계산
  - Item-Based CF
    - 모든 아이템 쌍에 대해 유사도 계산: $O(n^2 m’)$ 아이템 수는 $n$이고, 각 아이템이 받은 평점 수는 $m’$
- 공간 복잡도:
  - User-Based CF: $O(m^2)$
    모든 사용자 쌍에 대한 유사도 저장
  - Item-Based CF: $O(n^2)$
    모든 아이템 쌍에 대한 유사도 저장
- 일반적으론 $m \gg n$이므로, Item-Based CF가 더 효율적이다.
Computational Complexity of Online Phase:
- 시간 복잡도:
  - 유사도 top-K 이웃 기준 예측: $O(K)$
  - 전체 아이템에 대해 예측: $O(Kn)$
Comparing User-Based vs Item-Based CF:
- item-based는 user-based보다:
  - 더 관련선 높은 추천을 제공
  - 더 안정적(아이템 수는 상대적으로 더 고정적)
- user-based는 item-based보다:
  - 사용자 수 증가시 업데이트 비용이 큼
  - 새로운 사용자가 자주 추가되는 경우 비효율적
Strengths and Weaknesses of NB methods
- Strengths:
  - 직관적이고 이해하기 쉬움.
  - 사용자와 아이템 간의 관계를 명확하게 모델링.
- Weaknesses:
  - 희소성 문제: 사용자-아이템 상호작용 데이터가 희소할 경우 추천의 품질 저하.
  - 확장성 문제: 대규모 환경에서는 offline 계산 비용이 비현실적
Unified View of User-based & Item-based Methods
- User-based CF와 Item-based CF는 모두 사용자-아이템 평점 행렬을 기반으로 추천을 생성한다.
- 타겟 $(u, j)$에 대해,
  - 행과 열의 유사도를 결합하여 가장 유사한 평가값 탐색
  - 예측은 그 유사한 평가값들의 가중 평균으로 계산
- 사실상 회귀 모델의 변형
  - 휴리스틱 기반 회귀모델
- 문제점:
  - 아이템 간 상호의존성을 무시

Model-Based CF

Model-Based Collaborative Filtering은 사용자와 아이템 간의 상호작용 데이터를 기반으로 모델을 학습하여 추천을 생성하는 방법이다.
NB 방법과 달리, 모델 기반 방법은 사용자-아이템 평점 행렬을 직접 사용하지 않고, 학습된 모델을 사용하여 추천을 생성한다. 따라서 학습 데이터와 예측 데이터가 확실히 구분된다.

결정 트리, 룰 기반 모델, 신경망 등 다양한 모델을 사용할 수 있다.

Model-Based의 장점:
- 공간 효율성
  학습된 모델의 크기는 rating matrix보다 일반적으로 훨씬 작다.
- 속도
  NB 방법은 전처리 시간이 사용자/아이템 수에 대해 quadratic하게 증가하지만, 모델 기반 방법은 학습 후 예측이 빠르다.
- 과적합 방지
  모델 기반 방법은 일반적으로 더 강력한 일반화 능력을 가진다.

Latent Factor Models

Latent Factor Models은 rating matrix의 대부분의 row/column이 강한 상관관계를 갖기에, low-rank matrix로 근사하는 아이디어를 기반으로 한다.

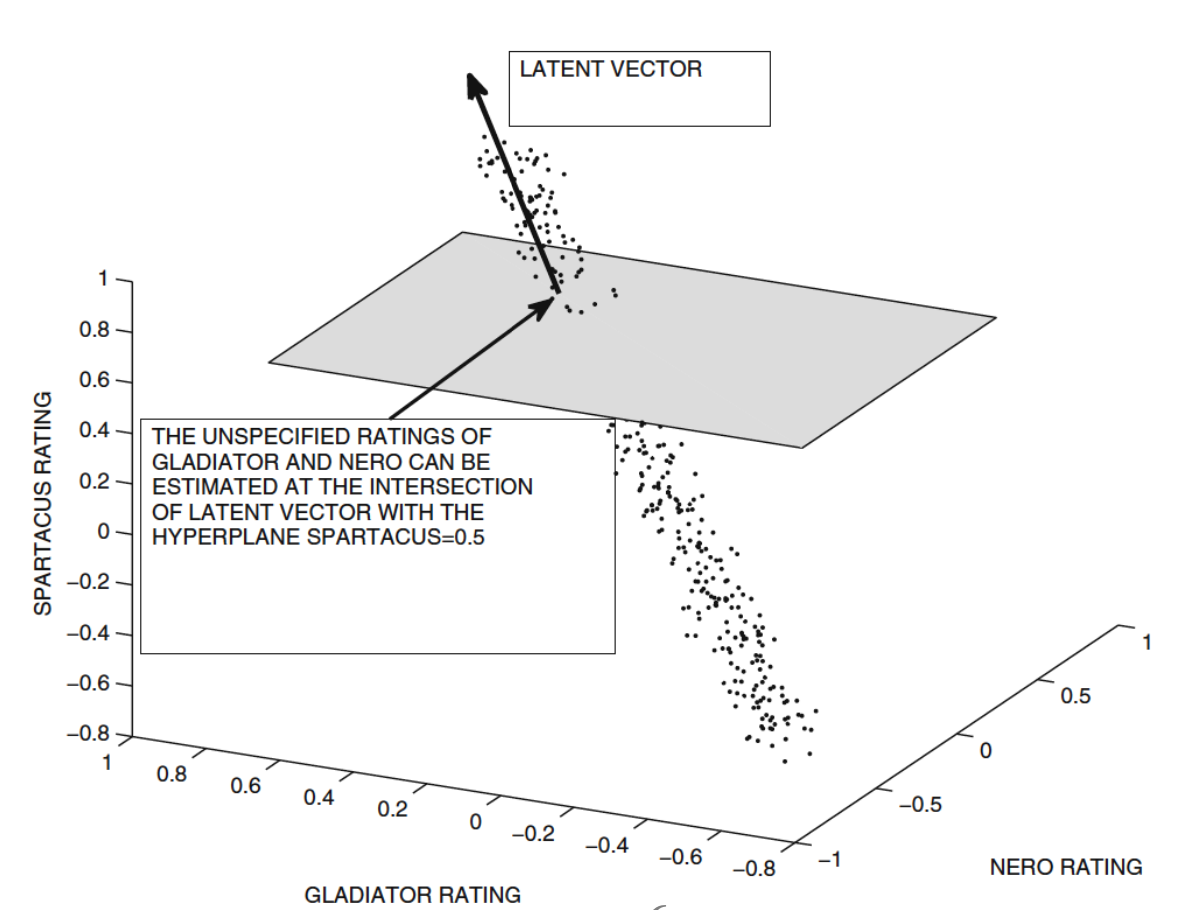
Geometric Intuition:
- 3개의 영화 rating($\in[-1,1]$)이 높은 상관관계를 갖는 경우, 3D scatter plot에서 이 점들은 1차원 직선 상에 위치한다.
- 노이즈가 없다면, 원래의 rating matrix의 rank는 1이다.
- 위 예시 그림에서, 영화 Spartacus의 rating이 0.5로 주어졌다면, 다른 영화들의 rating은 latent vector와 SPARTACUS Rating = 0.5의 hyperplane간의 교점으로 추정 가능하다
- 즉, $m \times n$ rating matrix의 rank가 $p \ll \min(m, n)$인 경우, 이 matrix는 $p$차원 hyperplane 위에 잘 표현될 수 있다
- 따라서 평균 제곱 거리(MSE)를 최소화하는 latent vector를 찾는 것이 목표가 된다.
- 만약 데이터에 상관관계가 거의 존재하지 않는다면, latent factor 모델은 잘 작동하지 않는다.
Low-Rank Approximation:
- 완전한 rating matrix $R$를 가정하면
- rank $k \ll \min(m, n)$인 행렬 $R$은 항상 $R \approx U V^T$로 표현될 수 있다.
  - $U \in \mathbb{R}^{m \times k}$, $V \in \mathbb{R}^{n \times k}$
- 실제로는 $rank(R) > k$인 경우가 많지만, 근사적으로 위와 같은 형태로 표현할 수 있다.
- 이때 오차는 Frobenius norm으로 측정된다. $||R - UV^T||_F^2 = \sum (r_{ij} - u_i^T v_j)^2$
Example:

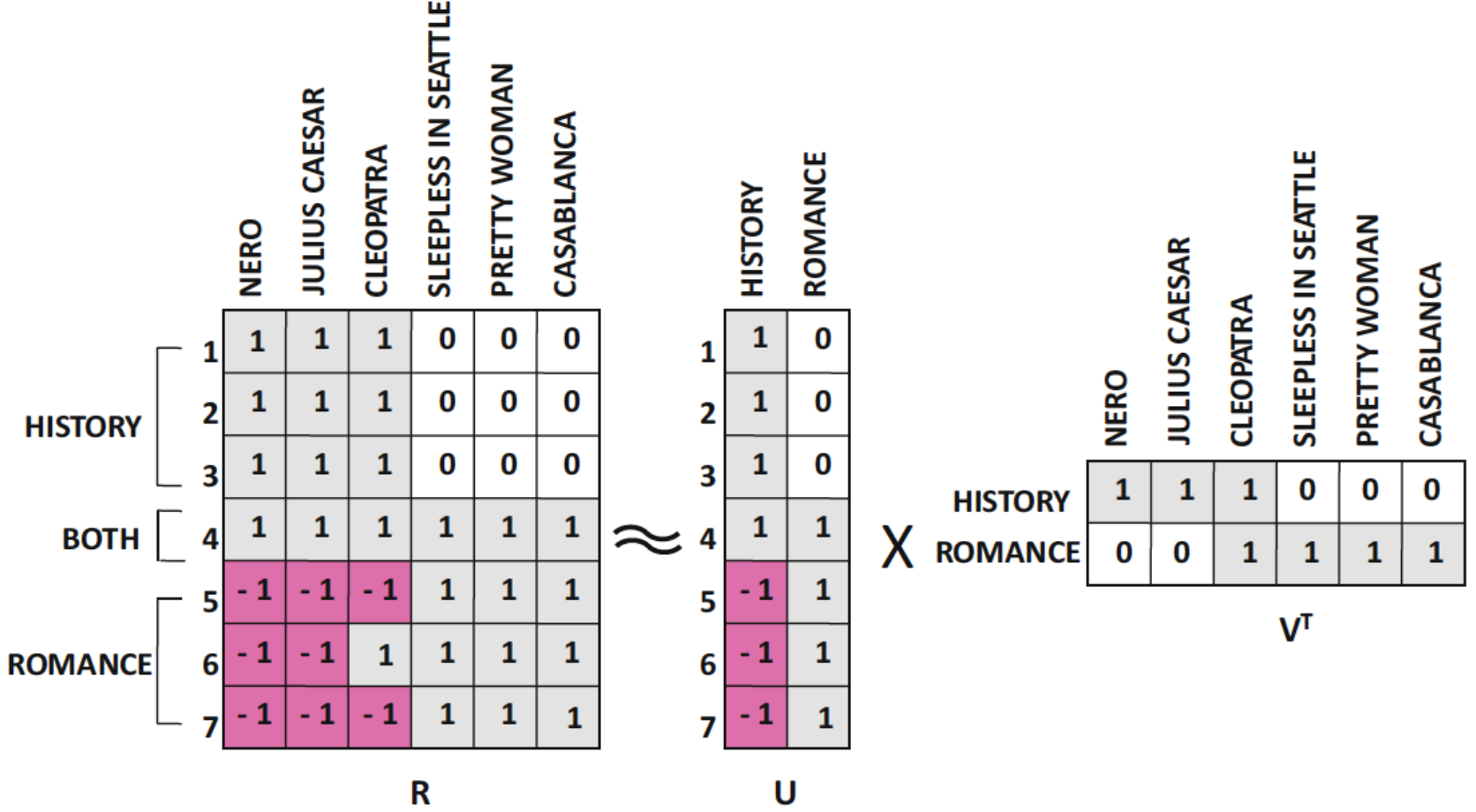
위 예시의 rating matrix는 7명의 사용자와 6개의 아이템(영화)에 대한 평점으로 구성되어 있다.(평점은 -1, 0, 1로 표현됨)

위 rating matrix를 rank 2로 근사하여 위와 같이 $R \approx UV^T$ 형태로 표현할 수 있다.
- $U$가 표현하게 되는 것은 사용자의 장르 성향이 되고
- $V$가 표현하게 되는 것은 영화의 장르 구성으로 해석할 수 있다.
- $U, V$의 행과 열은 각각 사용자와 아이템의 latent feature를 나타낸다.

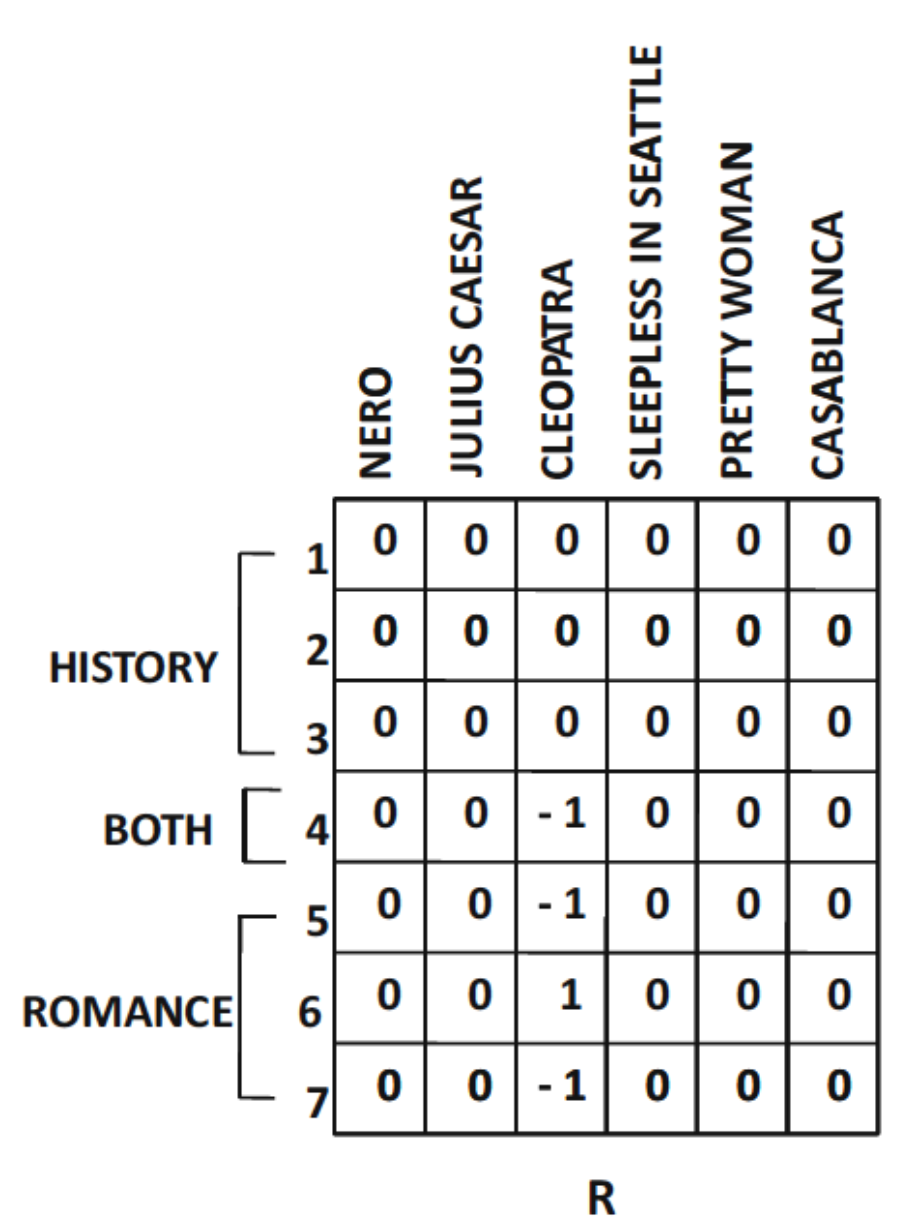
Residual matrix
- 위 예시에서는 패턴을 따르지 않는 Cleopatra 영화의 평점이 오차로 남는다.
Latent Factor의 의미 해석은 위 예시와 같이 항상 명확하게 해석되지는 않는다.
- 특히 양수값과 음수값이 혼합된 경우, latent factor의 의미를 해석하기 어려울 수 있다.
- 그럼에도, $U$와 $V$의 행과 열은 각각 사용자와 아이템 특성 간 주요 상관 구조를 의미하는 latent concept으로 이해 가능하다.
Incomplete Rating Matrix:
- 실제로는 rating matrix가 완전하지 않은 경우도 있지만, 데이터 내재적으로 중복된 구조가 존재한다면, 여전히 rank $k$로 근사할 수 있다.
Matrix Factorization Principle:
- $U, V$의 각 column:
  latent concept에 대한 latent vector
- $U, V$의 각 row:
  사용자와 아이템의 latent factor
- $\bar{u}_i$: $U$의 $i$번째 row
  사용자 $i$의 latent 개념에 대한 성향
- $\bar{v}_j$: $V$의 $j$번째 row
  아이템 $j$가 latent 개념들과 관련된 정도
Prediction:
- 사용자 $i$가 아이템 $j$에 대해 부여할 평점 $\hat{r}_{uj}$는 다음과 같이 계산된다.
  $\hat{r}_{ij} = \bar{u}_i^T \bar{v}_j$
- 즉, 사용자 $u$의 latent factor와 아이템 $j$의 latent factor 간의 내적을 통해 예측 평점을 계산한다.
Unconstrained Matrix Factorization:
- $U, V$를 학습하기 위해 MSE를 최소화하는 최적화 문제를 정의한다.
- 최적화 문제는 다음과 같이 표현된다.
  - $R$이 완전한 경우:
    $\min_{U, V} ||R - UV^T||_F^2$
    - 제약 조건 없음, Gradient Descent로 최적화 가능
  - $R$이 불완전한 경우: $\min_{U, V} \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - u_i^T v_j)^2$
    - $S$: 평가된 사용자-아이템 쌍의 집합
    - 이 역시 Gradient Descent로 최적화 가능
    - 파라미터 수: $m \times k + n \times k$ (사용자와 아이템의 latent factor 수)
Gradient Descent:
- $U, V$의 각 요소에 대해 편미분을 계산하여 업데이트한다.
- 목표함수 $J$에 대한 편미분
  $\frac{\partial J}{\partial u_{iq}} = \sum_{j: (i, j) \in S} (r_{ij} - u_i^T v_j)(-v_{jq}) = \sum_{j: (i, j) \in S} e_{ij} (-v_{jq})$ $\frac{\partial J}{\partial v_{jq}} = \sum_{i: (i, j) \in S} (r_{ij} - u_i^T v_j)(-u_{iq}) = \sum_{i: (i, j) \in S} e_{ij} (-u_{iq})$
- 여기서 $e_{ij} = r_{ij} - u_i^T v_j$는 예측 오차이다.
- Gradient Descent는 다음과 같이 업데이트된다.
  1. $U, V$를 무작위로 초기화
  2. 반복 수행:
    - 관측된 오차 $e_{ij}$ 계산
    - 사용자 u의 각 요소 업데이트: $u_{iq} ← u_{iq} + α ∑ e_{ij} v_{jq}$
    - 아이템 v의 각 요소 업데이트: $v_{jq} ← v_{jq} + α ∑ e_{ij} u_{iq}$
  3. 수렴 조건 확인
- Matrix Representation:
  - $E = R - UV^T$(only for $S$(observed entries))
  - 업데이트
    - $U ← U + α E V$
    - $V ← V + α E^T U$
Stochastic Gradient Descent (SGD):
- 전체 데이터셋을 사용하지 않고, 각 관측치에 대해 업데이트를 수행한다.
- 각 관측치에 대해 $u_i$와 $v_j$를 업데이트하는 방식으로 진행된다.
- 알고리즘:
  1. $U, V$ 무작위 초기화
  2. 반복:
    - 관측된 $S$ 셔플
    - 각 $(i,j)$에 대해: $e_{ij}$ 계산 각 $q$에 대해 $u_{iq}, v_{jq}$ 업데이트
  3. 수렴 조건 확인
Regularization:
- 과적합을 방지하기 위해 정규화 항을 추가한다.
- 최적화 문제는 다음과 같이 수정된다.
  $\min_{U, V} \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - u_i^T v_j)^2 + \frac{\lambda}{2} (\sum_{i=1}^m \sum_{s=1}^k u_{is}^2 + \sum_{j=1}^n \sum_{s=1}^k v_{js}^2)$
- 여기서 $\lambda$는 정규화 강도를 조절하는 하이퍼파라미터이다.
- 정규화 항은 각 요소의 제곱합을 포함하여, 모델의 복잡성을 줄이는 역할을 한다.
- partial derivative:
  $\frac{\partial J}{\partial u_{iq}} = \sum_{j: (i, j) \in S} e_{uj} (-v_{jq}) + \lambda u_{iq}$ $\frac{\partial J}{\partial v_{jq}} = \sum_{i: (i, j) \in S} e_{uj} (-u_{iq}) + \lambda v_{jq}$
- update formula:
  $u_{iq} ← u_{iq} + α (∑_{j: (i, j) \in S} e_{ij} v_{jq} - \lambda u_{iq})$ $v_{jq} ← v_{jq} + α (∑_{i: (i, j) \in S} e_{ij} u_{iq} - \lambda v_{jq})$
- matrix form:
  $U ← U + α (E V - λ U)$ $V ← V + α (E^T U - λ V)$
- 정규화 강도 $\lambda$ 선택법:
  - Hold-out method:
    - 데이터셋을 train, validation, test로 나누고, validation set에서 성능을 평가하여 가장 정확도가 높은 $\lambda$ 선택
  - Cross-validation:
    - K-fold cross-validation을 사용하여 $\lambda$의 최적값을 찾는다.
Incorporating Bias:
- 사용자와 아이템의 편향(bias)을 고려하여 모델을 개선할 수 있다.
- 전체 평점 행렬 $R$이 global mean을 중심으로 정규화된다고 가정.
- 사용자 $u$의 편향 $o_u$와 아이템 $j$의 편향 $p_j$를 추가하여 예측 평점을 다음과 같이 수정한다.
  $\hat{r}_{ij} = \bar{u}_i^T \bar{v}_j + o_u + p_j$
- 오차 계산:
  $e_{ij} = r_{ij} - (\bar{u}_i^T \bar{v}_j + o_u + p_j)$
- 목적 함수:
  $J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - (\bar{u}_i^T \bar{v}_j + o_u + p_j))^2 + \frac{\lambda}{2} (\sum_{i,s} u_{is}^2 + \sum_{j,s} v_{js}^2 + \sum_{i} o_i^2 + \sum_{j} p_j^2)$
  - 편향 변수들을 별도로 관리하지 않고, factor matrix의 크기를 $m \times (k+2), n \times (k+2)$로 확장하여 처리할 수 있다.
  - $U,V$의 마지막 두 열에 $o_i, p_j$를 추가하고, 그에 해당하는 요소에 1을 삽입
- 최적화 문제:
  $\min J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - \sum_{s=1}^{k+2} u_{is} v_{js})^2 + \frac{\lambda}{2} \sum_{s=1}^{k+2} (\sum_{i=1}^m u_{is}^2 + \sum_{j=1}^n v_{js}^2)$
  - 제약조건:
    - $V$의 $k+1$번째 열은 전부 1
    - $U$의 $k+2$번째 열은 전부 1
    - Gradient Descent시 해당 열들이 업데이트 되더라도 항상 1로 유지되도록 한다.
Incorporating Implicit Feedback:
- 사용자의 명시적 피드백뿐 아니라, 묵시적 피드백(예: 클릭, 조회 등)도 반영 가능
- SVD++ 또는 비대칭 factor 모델:
  - $V$: 명시적 피드백의 item factor
  - $Y$: 묵시적 피드백의 item factor
- 아이디어:
  - user factor는 명시적 피드백과 묵시적 피드백의 조합으로 형성
  - 사용자가 평가한 항목들의 implicit feedback을 고려하여 user factor를 생성
SVD++:
- 기존의 Matrix Factorization에 implicit feedback을 추가한 모델
- 수식:
  $R \approx (U + FY) V^T$
  - $U$: 명시적 피드백에 대한 사용자 factor
  - $F$: 사용자 x 아이템 implicit feedback matrix($m \times n$)
  - $Y$: implicit item x factor matrix($n \times (k+2)$)
- 역할:
  $FY$: 사용자가 선택적으로 평가한 항목들의 평균적인 latent factor, 이것을 $U$에 추가하여 implicit feedback을 반영
- 비용: 모델 유연성이 증가함에 따라 계산 비용이 증가
- 가정:
  - $R$: mean-centered rating matrix
  - user & item bias가 factor 행렬에 포함되어 있다고 가정(즉 $k+2$ 차원으로 확장됨)
- 예측:
  $\hat{r}_{ij} = \sum_{s=1}^{k+2} (u_{is} + \frac{1}{|I_i|} \sum_{h \in I_i} y_{hs}) v_{js}$
  - $I_i$: 사용자 $i$가 평가한 아이템 집합
  - $y_{hs}$: 아이템 $h$의 implicit factor
  - $v_{js}$: 아이템 $j$의 explicit factor
- 목적 함수:
  $\min J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - \hat{r}_{ij})^2 + \frac{\lambda}{2} \sum_{s=1}^{k+2} \left( \sum_{i=1}^m u_{is}^2 + \sum_{j=1}^n v_{js}^2 + \sum_{h=1}^n y_{hs}^2 \right)$
  - $U$의 $k+2$번째 열은 전부 1
  - $V$의 $k+1$번째 열은 전부 1
  - $Y$의 마지막 두 열은 전부 0
- 파라미터 업데이트:
  - 사용자 factor $u_{iq}$:
    $u_{iq} ← u_{iq} + α (e_{ij} v_{jq}- \lambda u_{iq})$
  - 아이템 factor $v_{jq}$: $v_{jq} ← v_{jq} + α (e_{ij} (u_{iq} + \frac{1}{\sqrt{|I_i|}} \sum_{h \in I_i} y_{hq}) - \lambda v_{jq})$
  - implicit factor $y_{hq}$:
    $y_{hq} ← y_{hq} + α (\frac{e_{ij}u_{iq}}{\sqrt{|I_i|}} - \lambda y_{hq})$
non-negative Matrix Factorization (NMF):
- NMF는 행렬의 모든 요소가 음수가 아닌 경우에만 적용되는 Matrix Factorization 기법이다.
- 해석이 용이함, unary matrix(e.g. 구매 유무)에서 유용하게 사용됨.
- 목적 함수:
  $\min_{U, V \geq 0, R \geq 0} ||R - UV^T||_F^2$
- 업데이트 방식:
  $u_{ij} ← \frac{(RV)_{ij}u_{ij}}{(U V^T V)_{ij}+ \epsilon}, \quad v_{ij} ← \frac{(R^T U)_{ij}v_{ij}}{(V U^T U)_{ij}+ \epsilon}$
  - $\epsilon$는 0으로 나누는 것을 방지하기 위한 작은 값
- 정규화 항 추가시:
  - 정규항:
    $\frac{\lambda_1}{2} ||U||_F^2 + \frac{\lambda_2}{2} ||V||_F^2$
  - 업데이트:
    $u_{ij} ← \max\left(0, \frac{(RV \lambda_1 U)_{ij} u_{ij}}{(U V^T V)_{ij} + \epsilon}\right), \quad v_{ij} ← \max\left(0, \frac{(R^T U \lambda_2 V)_{ij} v_{ij}}{(V U^T U)_{ij} + \epsilon}\right)$
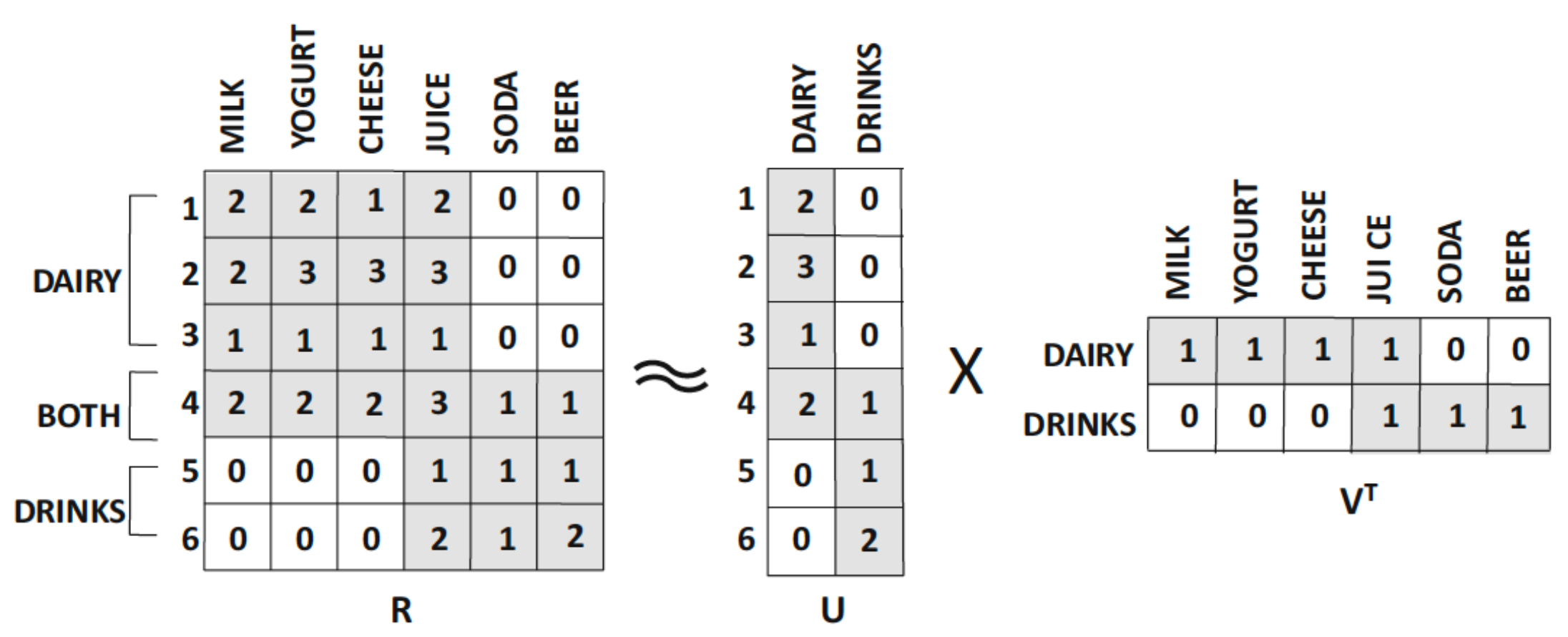
- NMF의 해석력
  - 아래 예시는 고객이 구매한 수량을 기준으로 행렬이 구성되어 있다.
  - NMF로 분해하면, $U$(고객 latent factor)와 $V$(상품 latent factor)가 도출된다.
  - 결과적으로 $r_{ij} \approx \sum_{s=1}^{k} u_{is} v_{js}$에 대해 다음과 같은 해석이 가능하다.
    $r_{ij} \approx (\text{고객 } i \text{의 } \text{유제품에 대한 선호도}) \times (\text{상품 } j \text{의 유제품 특성}) + (\text{고객 } i \text{의 } \text{음료에 대한 선호도}) \times (\text{상품 } j \text{의 음료 특성})$

rank-K matrix factorization $UV^T$는 다음과 같이 k개의 구성요소로 분해될 수 있다.
- $UV^T = \sum_{i=1}^{k} U_i V_i^T$
- $U_i$: $U$의 $i$번째 column
- $V_i$: $V$의 $i$번째 column
- 각 $m \times n$ 행렬 $U_i V_i^T$는 $i$번째 latent factor에 얼마나 강하게 연결되어 있는지를 나타낸다.

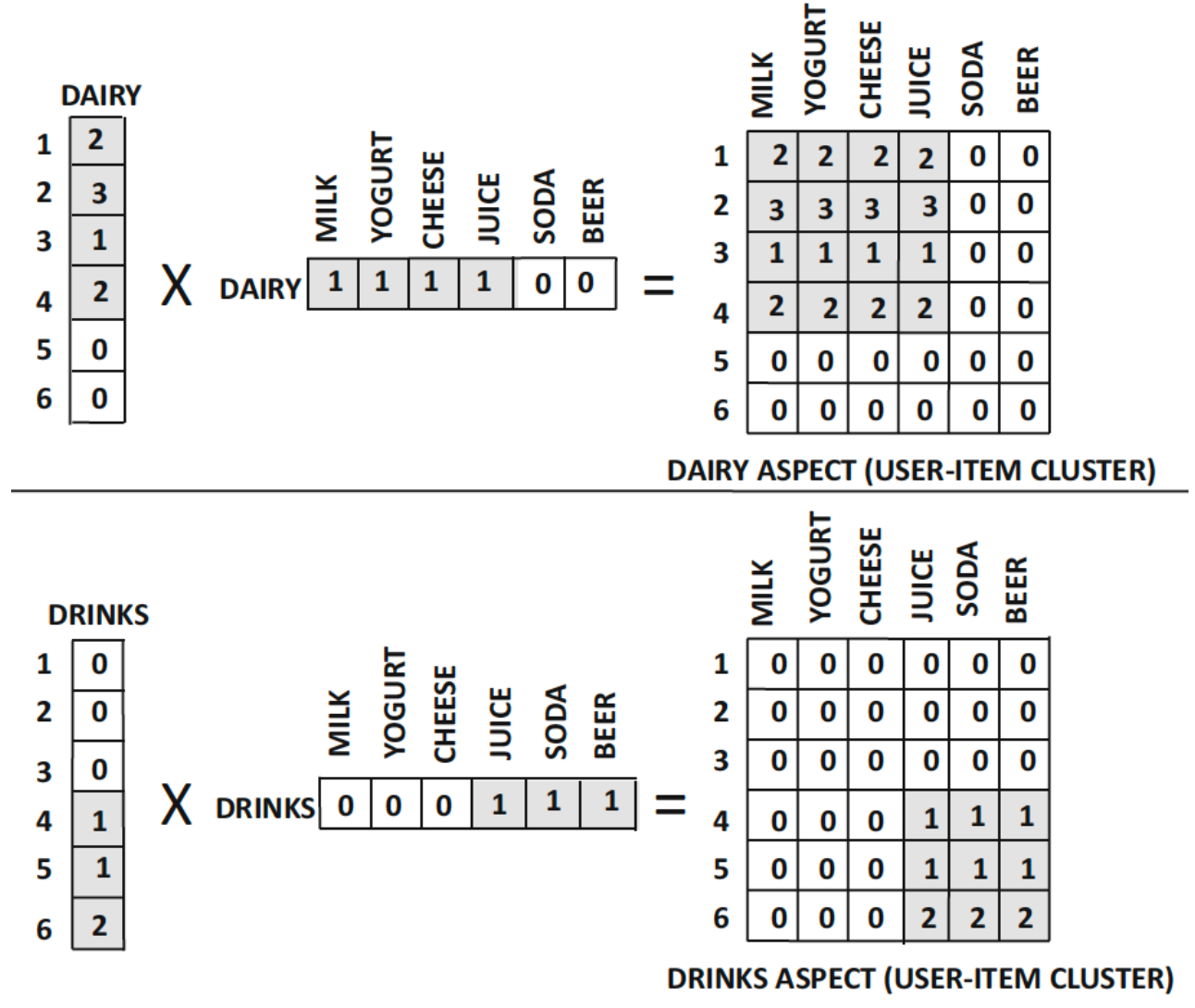
NMF Components — Dairy, Drink aspect에 대한 사용자-아이템 선호

NMF는 implicit feedback에 대해서도 적용 가능하다.
- 구매 기록이 없으면 0(negative feedback)으로 간주
- 그렇지 않으면 unobserved entry에 대한 오차가 커져 overfitting이 발생할 수 있다.
- 특히 unary 행렬에 대해서는 0 취급이 타당함
Issues with implicit feedback:
- missing을 0으로 간주할때, 전체 학습이 0 데이터에 지배될 수 있음(class imbalance 문제)
- Ensemble approach:
  - 0 샘플링: 전체 0 데이터 중 일부를 샘플링하여 학습에 사용
  - 해당 과정을 여러번 반복하여 모델을 학습하고, 최종 예측은 여러 모델의 평균으로 계산
  - 다양한 관점의 학습이 가능
- Weighting approach:
  - 0 데이터에 가중치를 부여하여 학습
  - $w_{ij} = 1 + \theta \cdot r_{ij}$ 형태로 가중치 설정
    - $r_{ij}$가 1일때 보다 큰 값을 가짐
Ratings with both likes and dislikes:
- 평점이 1부터 5일때, 1은 매우 비선호, 5는 매우 선호를 나타냄
- 이 경우, missing entry를 0으로 간주하는 것이 적절하지 않음
- 따라서 반드시 관측된 entry set $S$에 대해서만 학습을 수행해야 함
- SGD와 같은 방식을 사용할 수 있지만, non-negative constraint를 추가해야 함(즉, 업데이트 후 음수값이 나온다면 0으로 설정)
- 이 경우에선 NMF의 해석 가능성이 사라진다
  - unary의 경우, 0은 비선호를 의미하지만, 평점이 있는 경우에는 0이 중립적인 상태를 나타내기 때문

Intergrating Factorization and Neighborhood Methods

Understanding Matrix Factorization family:
- 목표: $R \approx UV^T$
- 다양한 제약조건을 부여하면 해석 가능성을 높일 수 있다.
- 제약 조건을 넣으면 분산은 줄지만, 편향이 증가한다.
- 하지만 이로 인해 모델의 일반화 성능은 향상됨
Non-personalized bias centric model:
- 모든 사용자와 아이템에 대해 동일한 편향을 적용하는 모델
- 예측 평점은 다음과 같이 계산된다.
  $\hat{r}_{ij} = + b_i^{user} + b_j^{item}$
- $b_i^{user}$: 사용자 $i$의 편향(사용자의 관대함)
- $b_j^{item}$: 아이템 $j$의 편향(아이템의 인기)
- 이 모델은 사용자와 아이템 간의 상호작용을 고려하지 않으며, 단순히 평균과 편향만을 사용하여 예측한다.
- 목적 함수:
  $J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - \hat{r}_{ij})^2 + \frac{\lambda}{2} (\sum_{i=1}^m (b_i^{user})^2 + \sum_{j=1}^n (b_j^{item})^2)$
- Gradient Descent:
  $b_i^{user} ← b_i^{user} + α (e_{ij} - \lambda b_i^{user})$ $b_j^{item} ← b_j^{item} + α (e_{ij} - \lambda b_j^{item})$
- $\hat{r}{ij}$를 계산해 Bias Matrix $B{ij}$로 저장
- 이후 다른 모델에서 이 Bias Matrix를 사용하여 예측 평점을 보정할 수 있음
- $r_{ij} - B_{ij}$ 계산해 이 residual을 개인화된 정보로 학습 가능(Robustness 향상)
Item-Based Model과 Latent Factor Model의 결합:
$\hat{r}_{ij} = b_i^{user} + b_j^{item} + \frac{\sum_{l \in Q_j(i) w_{lj}^{item} (r_{il} - b_i^{user} - b_i^{item})}}{\sqrt{|Q_j(i)|}}$
- $b_i^{user}$: 사용자 $i$의 편향
- $b_j^{item}$: 아이템 $j$의 편향
- $Q_j(i)$: 사용자 $i$가 평가한 아이템 $j$와 유사한 k개의 아이템 집합
- $w_{lj}^{item}$: 아이템 간의 유사도 가중치
- 즉, 사용자 $i$가 평가한 아이템 $j$ 주변의 유사한 아이템들의 평점을 기반으로 예측 평점을 계산한다.
- Gradient Descent:
  $b_i^{user} ← b_i^{user} + α (e_{ij} - \lambda b_i^{user})$ $w_{lj}^{item} ← w_{lj}^{item} + α_2(\frac{e_{ij} (r_{il} - B_{il})}{\sqrt{|Q_j(i)|}} - \lambda w_{lj}^{item})$
- Implicit feedback 보강:
  - $c_{lj}$ : 아이템 $l$과 $j$이 함께 평가된 정도
  - 많을수록 $r_{ij}$에 대한 영향력이 커져야함
    $\frac{\sum_{l \in Q_j(i)} c_{lj}}{\sqrt{|Q_j(i)|}}$
- 최종 예측 평점:
  $\hat{r}_{ij} = b_i^{user} + b_j^{item} + \frac{\sum_{l \in Q_j(i)} w_{lj}^{item} (r_{il} - b_i^{user} - b_l^{item})}{\sqrt{|Q_j(i)|}} + \frac{\sum_{l \in Q_j(i)} c_{lj}}{\sqrt{|Q_j(i)|}}$
Latent Factor Model과 Neighborhood Model의 결합:
- Latent factor model을 neighborhood model에 통합하여, 사용자와 아이템 간의 latent factor를 neighborhood 정보로 활용한다. $\hat{r}_{ij} = \underbrace{ \sum_{l \in Q_j(i)} \frac{w_{lj}^{\text{item}} \cdot (r_{il} - B_{il})}{\sqrt{|Q_j(i)|}} + \sum_{l \in Q_j(i)} \frac{c_{lj}}{\sqrt{|Q_j(i)|}} }_{\text{Neighborhood Component}} + \underbrace{ \left( u_i + \sum_{h \in I_i} \frac{y_{hs}}{\sqrt{|I_i|}} \right) \cdot v_j }_{\text{Latent Factor Component + Bias}}$
- $b_i^{user}$와 $b_j^{item}$은 latent factor 모델의 bias로 대체
- 최적화 모델:
  $\min J = \frac{1}{2} \sum_{(i, j) \in S} (r_{ij} - \hat{r}_{ij})^2 + \frac{\lambda}{2} \sum_{s=1}^{k+2} \left( \sum_{i=1}^m u_{is}^2 + \sum_{j=1}^n v_{js}^2 + \sum_{j=1}^n y_{js}^2 \right) + \frac{\lambda_2}{2} \sum_{j=1}^n \sum_{l \in Q_j(i)} [(w_{lj}^{\text{item}})^2 + (c_{lj})^2]$
  - 제약조건:
    - $U$의 $k+2$번째 열은 전부 1
    - $V$의 $k+1$번째 열은 전부 1
    - $Y$의 마지막 두 열은 전부 0
- Gradient Descent:
  $u_{iq} ← u_{iq} + α (e_{ij} v_{jq} - \lambda u_{iq})$ $v_{jq} ← v_{jq} + α (e_{ij} (u_{iq} + \frac{1}{\sqrt{|I_i|}} \sum_{h \in I_i} y_{hq}) - \lambda v_{jq})$ $y_{hq} ← y_{hq} + α (\frac{e_{ij} u_{iq}}{\sqrt{|I_i|}} - \lambda y_{hq})$ $w_{lj}^{\text{item}} ← w_{lj}^{\text{item}} + α_2(\frac{e_{ij} (r_{il} - B_{il})}{\sqrt{|Q_j(i)|}} - \lambda_2 w_{lj}^{\text{item}})$ $c_{lj} ← c_{lj} + α_2(\frac{e_{ij}}{\sqrt{|Q_j(i)|}} - \lambda_2 c_{lj})$

Classification vs Collaborative Filtering

Classification:
- 주어진 입력에 대해 특정 클래스를 예측하는 문제.
- 예: 이메일이 스팸인지 아닌지 분류하는 문제.
- 입력과 출력이 명확하게 정의되어 있다.
Collaborative Filtering:
- 사용자와 아이템 간의 상호작용 데이터를 기반으로 추천을 생성하는 문제.
- 독립 변수와 종속 변수가 명확하게 정의되지 않으며, 사용자와 아이템 간의 관계를 모델링한다.

Content-Based Filtering

Content-Based Filtering은 아이템의 속성을 기반으로 추천을 생성하는 방법이다.
과거 사용자의 선호도를 분석하여 유사한 아이템을 추천한다.

Data:
- 아이템의 속성 데이터(예: 텍스트, 이미지, 오디오 등).
- 사용자 피드백(예: 평점, 클릭 등).
Steps:
1. 전처리 및 특징 추출(아이템의 속성을 벡터로 표현).
  예: 텍스트 아이템의 경우 TF-IDF, Word2Vec 등을 사용하여 벡터화.
2. 사용자 프로필 학습
  각 사용자마다 아이템의 속성을 기반으로 user-specific 모델을 학습.
  모델은 사용자의 관심(평점, 클릭 등)을 아이템의 속성과 연결.
  학습된 모델을 user-profile이라고 한다.
3. 사용자 프로필과 아이템 속성 간의 유사도를 계산 & 유사도가 높은 아이템을 추천.
When to Use Content-Based Filtering:
- 아이템의 속성이 중요할 때(예: 영화, 음악, 책 등).
- 다른 사용자 평가가 부족할 때
Pros & Cons:
- Pros:
  - 사용자 선호도에 대한 명확한 설명 가능성.
  - 새로운 아이템에 대한 추천이 용이.
- Cons:
  - 아이템의 속성 데이터가 필요.(텍스트가 없다면 아이템 특성 추출이 어려움)
  - 사용자 프로필이 없으면 추천 불가(Cold Start Problem).
  - 과도한 개인화로 인해 추천의 다양성이 떨어질 수 있다.

Knowledge-Based Recommender Systems

Knowledge-Based Recommender Systems는 사용자와 아이템 간의 상호작용 데이터 없이도 추천을 생성할 수 있는 방법이다.

Data:
- 사용자 요구사항(예: 선호하는 아이템의 특성).
- 아이템의 속성 데이터.
Constraint-Based Filtering:
- 사용자의 요구사항을 만족하는 아이템을 추천.
- 예: 사용자가 특정 가격대의 상품을 원할 때, 해당 가격대의 상품을 추천.
Case-Based Reasoning:
- 사용자가 제시한 특정 사례를 기반으로 유사한 사례를 찾아 추천.

Hybrid Recommender Systems

Hybrid Recommender Systems는 여러 추천 방법을 결합하여 추천의 품질을 향상시키는 방법이다.

결합 방식:
- Weighted Hybrid: 각 추천 방법의 결과를 가중치로 결합.
- Hybrid Model: 여러 추천 방법을 하나의 모델로 통합.

Evaluation of Recomendor Systems

추천 시스템은 분류(Classification) 또는 회귀(Regression) 문제와 유사하게 평가할 수 있다.

예측 성능 -> 정답 평점과 예측 평점 간의 차이를 측정.
주요 평가 지표:
- ABS: 절대 오차(Absolute Error)
  - 예측 평점과 실제 평점 간의 절대 차이.
    $ABS = \frac{1}{|\mathcal{U}||\mathcal{I}|} \sum_{u \in \mathcal{U}, i \in \mathcal{I}} |r_{ui} - \hat{r}_{ui}|$
  - $\mathcal{U}$: 사용자 집합
  - $\mathcal{I}$: 아이템 집합
  - $r_{ui}$: 사용자 $u$가 아이템 $i$에 부여한 실제 평점
  - $\hat{r}_{ui}$: 사용자 $u$가 아이템 $i$에 대해 예측한 평점
- MAE: 평균 절대 오차(Mean Absolute Error)
  - 모든 사용자에 대한 ABS의 평균.
    $MAE = \frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \sum_{i \in \mathcal{I}} |r_{ui} - \hat{r}_{ui}|$
- precision, recall, f1-score 등은 추천 시스템의 평가지표로 사용하기엔 너무 엄격하다.

Domain Based Recommender Systems

Context-Aware Recommender Systems:
- 사용자의 현재 상황(예: 위치, 시간 등)을 고려하여 추천.
- 예: 사용자가 특정 장소에 있을 때 해당 장소와 관련된 아이템을 추천.
Time-Sensitive Recommender Systems:
- 시간에 따라 사용자 선호도가 변할 수 있음을 고려하여 추천.
- 예: 계절에 따라 선호하는 아이템이 달라질 수 있다.
Location-Based Recommender Systems:
- 사용자의 위치 정보를 활용하여 추천.
- 예: 사용자가 특정 지역에 있을 때 해당 지역의 아이템을 추천.
Social Recommender Systems:
- 사용자의 소셜 네트워크 정보를 활용하여 추천.
- 예: 페이스북 친구 추천

Advanced Topics

Cold Start Problem: 신규 사용자/아이템 → content/knowledge 기반이 더 강함
Attack-Resistant RS: 악의적 평점 조작 대응
Group RS: 여러 사용자에 대한 추천 (가족, 팀 등)
Multi-Criteria RS: 다양한 기준에 따라 평가 (예: 영화 스토리 vs 음악)
Active Learning: 정보 부족할 때 추가 평점 요청으로 보완
Nonintrusiveness: 사용자에게 부담 없이 암묵적 데이터 수집 (클릭, 읽는 시간 등)
Privacy: 민감한 정보 활용에 대한 보안 및 프라이버시 문제

해당 포스트는 서울대학교 산업공학과 박종헌 교수님의 데이터관리와 분석 25-1학기 강의를 정리한 내용입니다.

인공지능, 추천시스템

추천시스템 강의정리

This post is licensed under CC BY 4.0 by the author.